https://www.zhihu.com/question/59156172/answer/168224345

退役正好一年了。把回忆录补完。

肯定有退役的oier很疑惑高三该怎么过。希望能帮到大家。

集训队爷就不用D我这个蒟蒻了qaq

http://trinkle.is-programmer.com/2015/7/21/memory.112423.html

广告：https://pan.baidu.com/s/1o8kyBEE 请各位大爷们免费品尝

或许辛普森积分要成为时代的眼泪了？

格林公式大法好 orzakf

$$\iint_{D}\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=\oint_{C} P dx+Q dy$$ $$let \ P=-y,\ Q=x$$ $$\iint_{D}2 dx dy=\oint_{C} x dy-y dx$$

$Circle(x_0,y_0,r):$

$$\begin{cases}x=x_0+r\cdot cos\theta \\ y=y_0+r\cdot sin\theta\end{cases}$$

设边界端点从$\theta_1$到$\theta_2$（逆时针方向）

$$\begin{eqnarray}S&=&\iint_{D}1 dx dy\\&=&\frac{1}{2}\oint_{C}xdy-ydx\\&=&\frac{1}{2}\int_{\theta_1}^{\theta_2} (x_0+r\cdot cos\theta)d(y_0+r\cdot sin\theta)-(y_0+r\cdot sin\theta)d(x_0+r\cdot cos\theta)\\&=&\frac{r}{2}\int_{\theta_1}^{\theta_2} [(x_0+r\cdot cos\theta)\cdot cos\theta +(y_0+r\cdot sin\theta)\cdot sin\theta ]d\theta\\&=&\frac{r}{2}\int_{\theta_1}^{\theta_2} [x_0\cdot cos\theta + y_0\cdot sin\theta+r]d\theta\\&=&\frac{1}{2}\cdot(f(r,x_0,y_0,\theta_2)-f(r,x_0,y_0,\theta_1))\end{eqnarray}$$

其中

$$f(r,x,y,\theta)=r^2\cdot \theta+r\cdot x\cdot sin\theta-r\cdot y\cdot cos\theta$$

所以对于圆并，只要对于每个圆，求出它在最终图形里面所占的边界，然后加起来就好了

复杂度：$O(n^2\cdot log(n))$

直线也是类似的，式子还比这个更简单

代码比扫描线短了不少2333

BZOJ2178:

/**************************************************************
    Problem: 2178
    User: wjy1998
    Language: C++
    Result: Accepted
    Time:684 ms
    Memory:868 kb
****************************************************************/

#include<cmath>
#include<cstdio>
#include<algorithm>

typedef double ld;

const int N = 1010;
const ld pi = acos(-1);

int n; ld ans;

struct P {
    ld x, y;
    P operator - (const P&a) const {
        return (P) {x - a.x, y - a.y};
    }
    ld len () {
        return sqrt(x * x + y * y);
    }
};

struct C {
    P o; ld r;
    bool operator < (const C&a) const {
        if (o.x != a.o.x) return o.x < a.o.x;
        if (o.y != a.o.y) return o.y < a.o.y;
        return r < a.r;
    }
    bool operator == (const C&a) const {
        return o.x == a.o.x && o.y == a.o.y && r == a.r;
    }
    ld oint (ld t1, ld t2) {
        return r * (r * (t2 - t1) + o.x * (sin(t2) - sin(t1)) - o.y * (cos(t2) - cos(t1)));
    }
} a[N];

struct D {
    ld x; int c;
    bool operator < (const D&a) const {
        return x < a.x;
    }
} pos[N * 2];

ld work (int c) {
    int tot = 0, cnt = 0;
    for (int i = 1; i <= n; i++)
    if (i != c) {
        P d = a[i].o - a[c].o; ld dis = d.len();
        if (a[c].r <= a[i].r - dis) return 0;
        if (a[i].r <= a[c].r - dis || a[i].r + a[c].r <= dis) continue;
        ld g = atan2(d.y, d.x), g0 = acos((dis * dis + a[c].r * a[c].r - a[i].r * a[i].r) / (2 * dis * a[c].r)), l = g - g0, r = g + g0;
        if (l < -pi) l += pi * 2;
        if (r >= pi) r -= pi * 2;
        if (l > r) cnt++;
        pos[++tot] = (D) {l, 1};
        pos[++tot] = (D) {r, -1};
    }
    pos[0].x = -pi, pos[++tot].x = pi;
    std::sort(pos + 1, pos + 1 + tot);
    ld ans = 0;
    for (int i = 1; i <= tot; cnt += pos[i++].c)
        if (cnt == 0) ans += a[c].oint(pos[i - 1].x, pos[i].x);
    return ans;
}

int main () {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%lf%lf%lf",&a[i].o.x, &a[i].o.y, &a[i].r);
    std::sort(a + 1, a + 1 + n);
    n = std::unique(a + 1, a + 1 + n) - a - 1;
    for (int i = 1; i <= n; i++) ans += work(i);
    printf("%.3lf\n", ans / 2);
}

广告：同情一下一只退役多年的高考狗...

戳我

希望能帮到大家

Rank1已经不再重要

新的征程就在前方

Codechef July Challenge 2015 » NTHCIR

虽然我知道在比赛还没结束前挂题解不好，但是还是想骗一发访问量。

题目大概是这样的：

有很多圆，满足 $C_n(n\ge 4)$ 与 $C_1,C_2,\cdots ,C_{n-1}$ 都相切，$C_3$ 与 $C_1,C_2$ 相切，$C_2$ 与 $C_1$ 相切，图形如下：

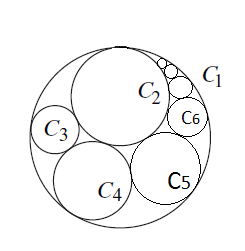
现已知 $r_1,r_2,r_3,r_4$，求 $r_n$。询问数<=1000w，$n\le 10^9$，时限 $1.5s$

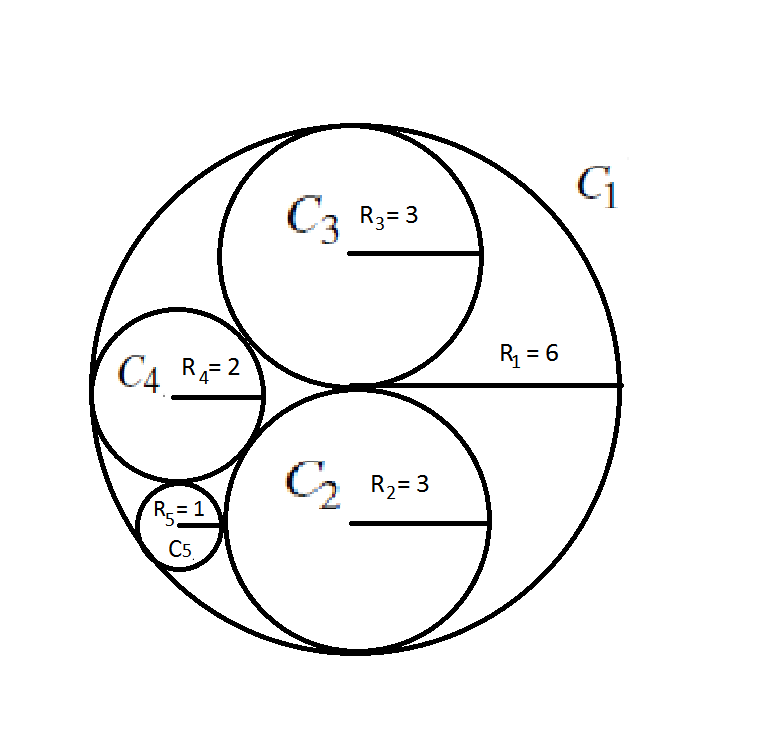
例如：当 $r_1=6,r_2=r_3=3,r_4=2$ 的时候，圆大概长这样：

圆的反演是什么呢？

我们先选定一个点 $O$为反演中心，以 $O$ 为圆心，半径为 $r$ 画一个圆。然后对于平面上的点 $P$ 和 $P'$，如果 $P$ 和 $P'$ 在以 $O$ 为起点的射线上，并且 $|OP|\cdot|OP'|=r^2$，那么就说 $P$ 和 $P'$ 互为反演点。

所以圆外的点反演一下会到圆内，圆内会到圆外，圆上则不变。

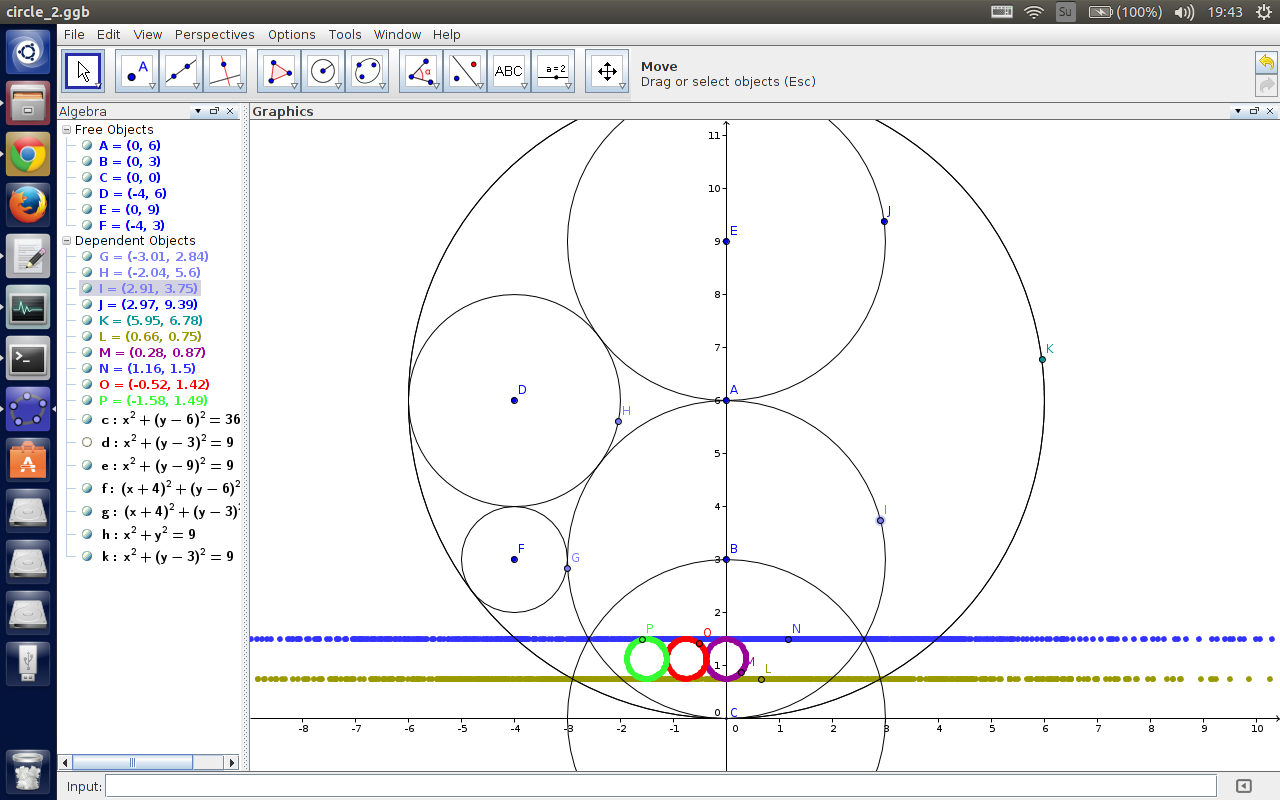
我找了 $GeoGebra$ 来玩玩，效果差不多是长下面这个样子的：

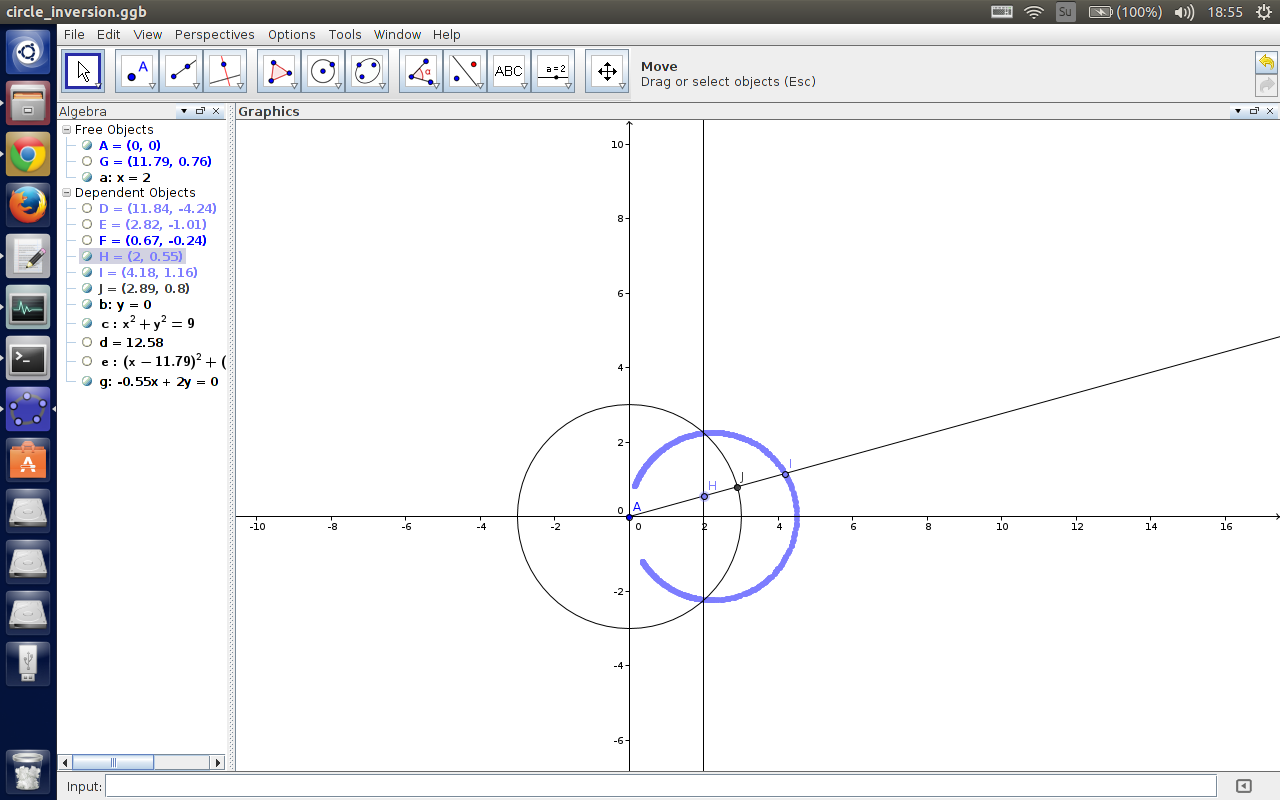
反演中心为坐标原点，点 $H$ 在直线上移动，点 $J$ 为射线 $AH$的焦点，点 $I$ 为点 $H$ 的反演点。

可以看到，一条不过反演中心的直线反演之后变成了一个过反演中心的圆。而且直线和两个圆两两相交。

由于反演的可逆性，这个圆反演一下就变成了一条直线啦~

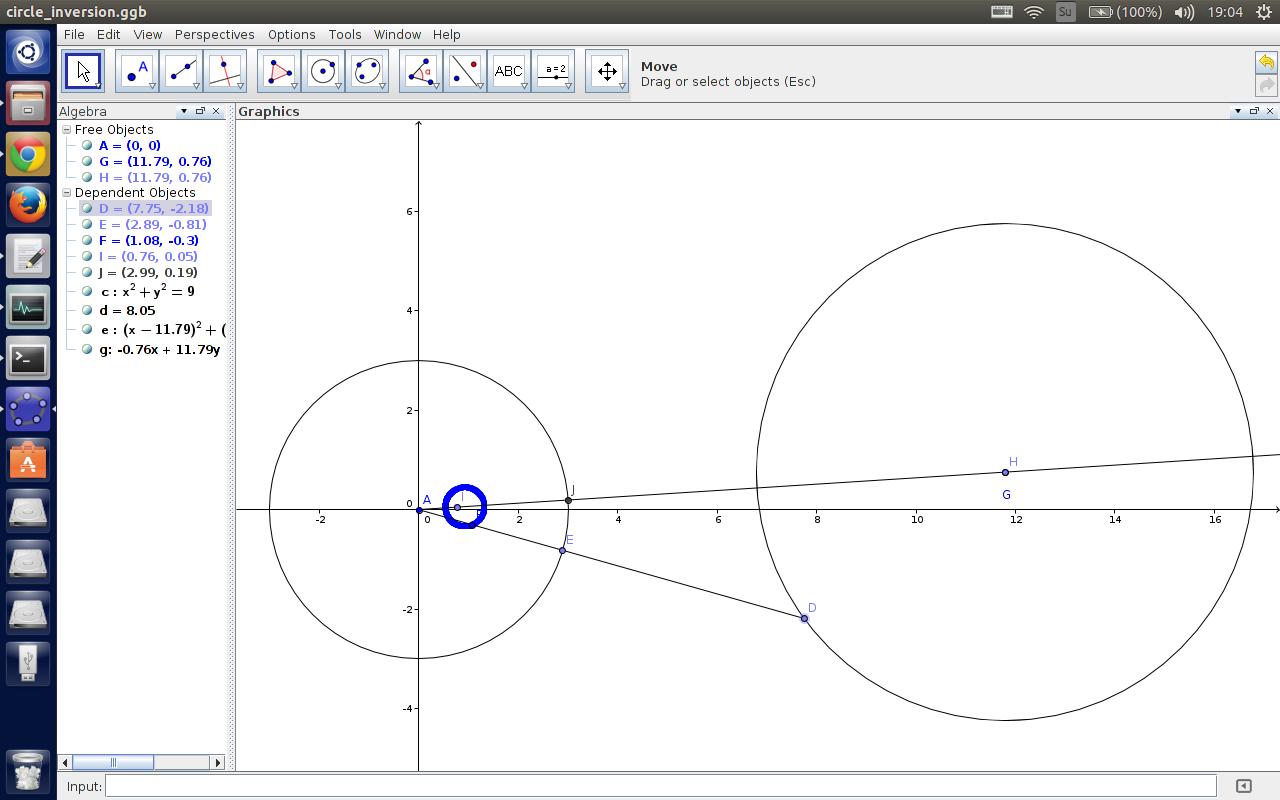
一个不过反演中心的圆反演以后是一个以反演中心位似的圆。

从上面的图来看，显然两个圆是反过来对应的，并不是直接位似。还有切记，圆心反演完以后并不是反演完的圆的圆心，比如上面的点 $H$ 和 $I$。

再来一个好玩点的：

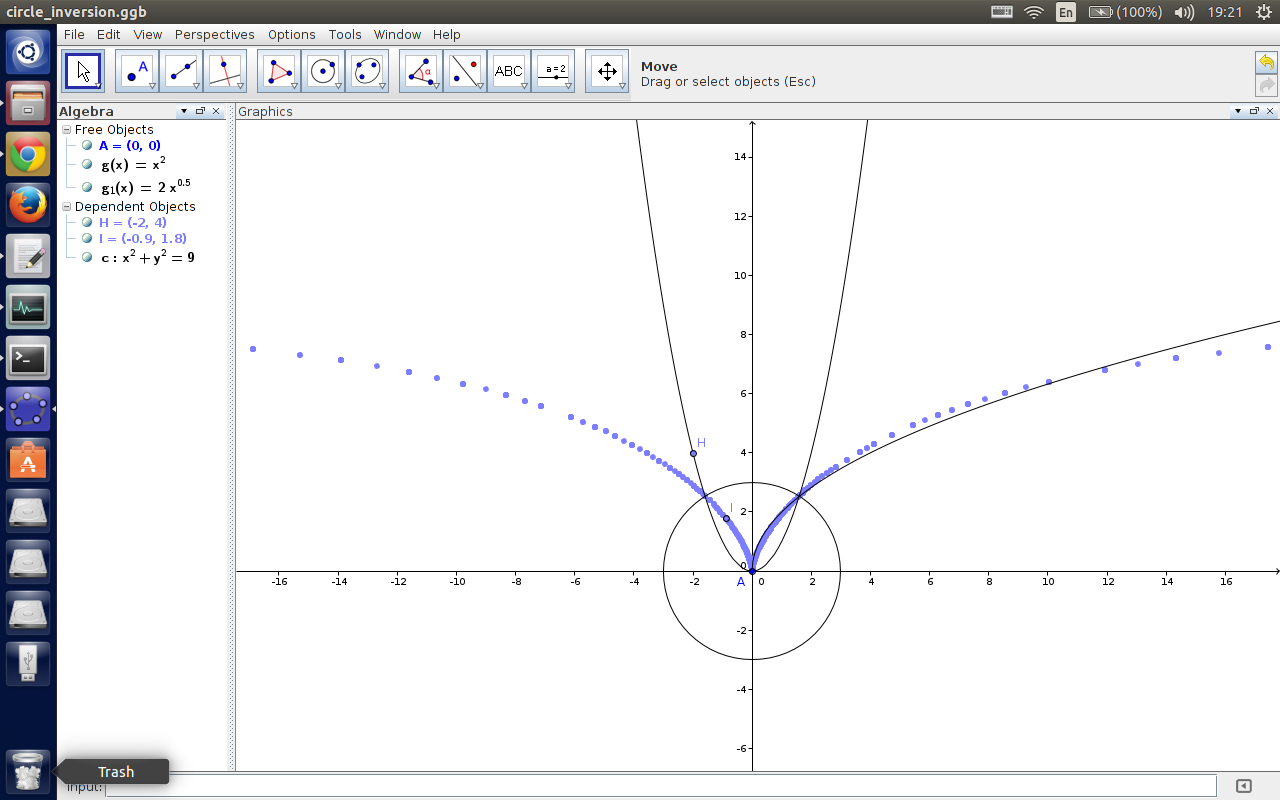
抛物线反演一下，不知道变成了什么。。。右边的黑线是 $2\sqrt{x}$，然而不能拟合。

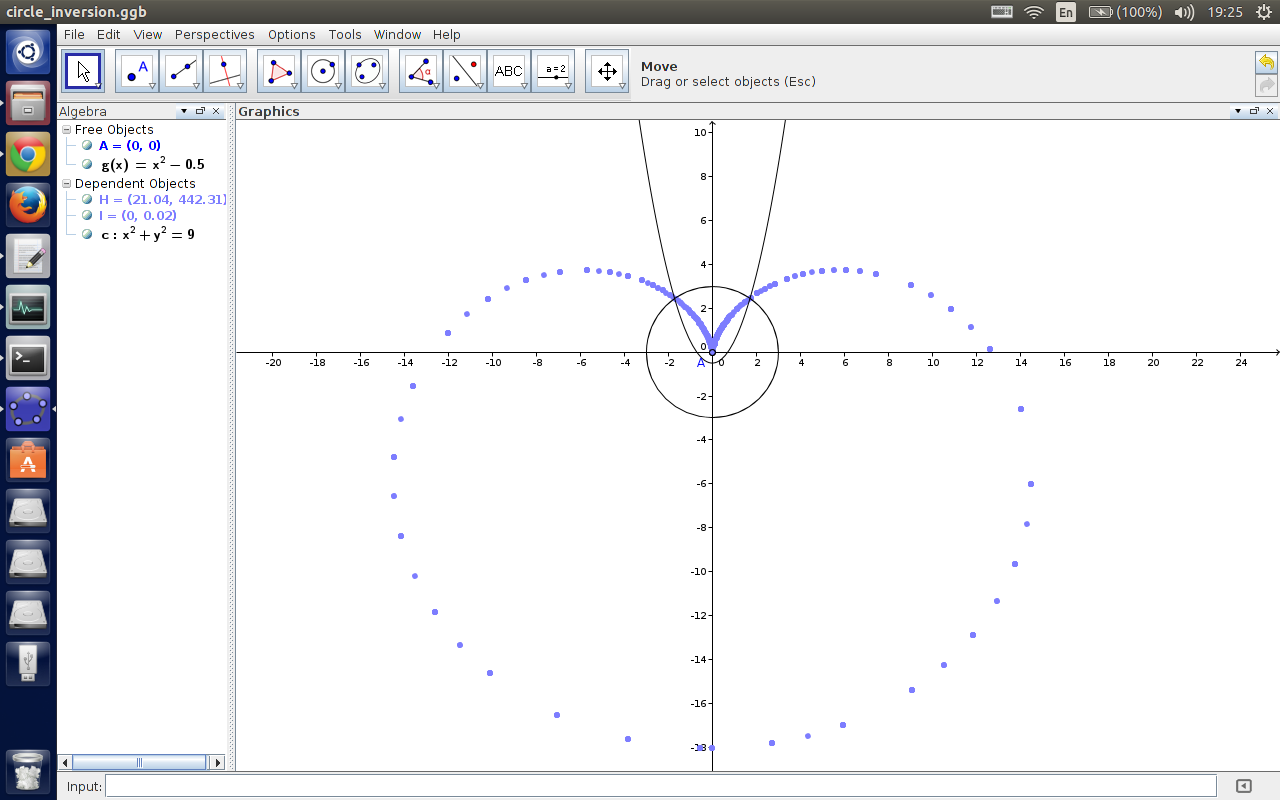
然后稍微往下移一点就变成了心型线！

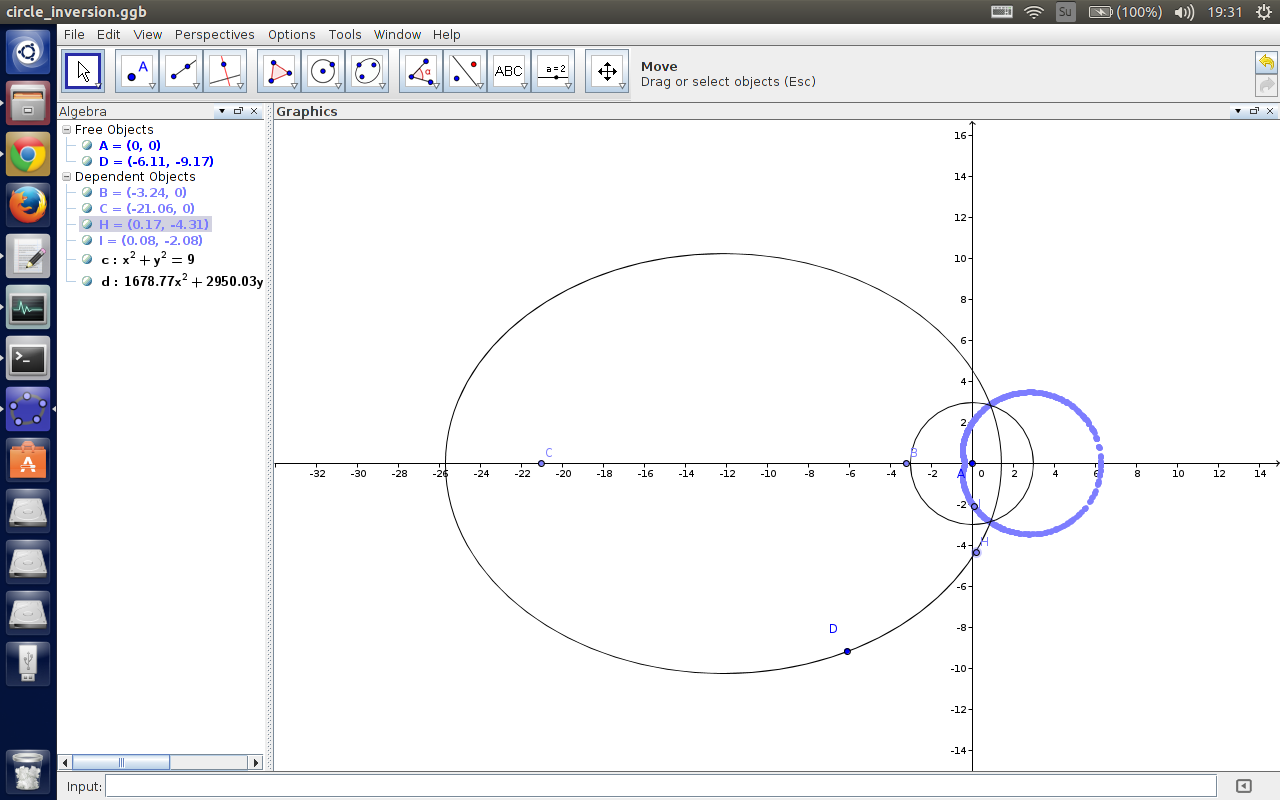
椭圆好像跟上面两种差不多，不是太好玩。

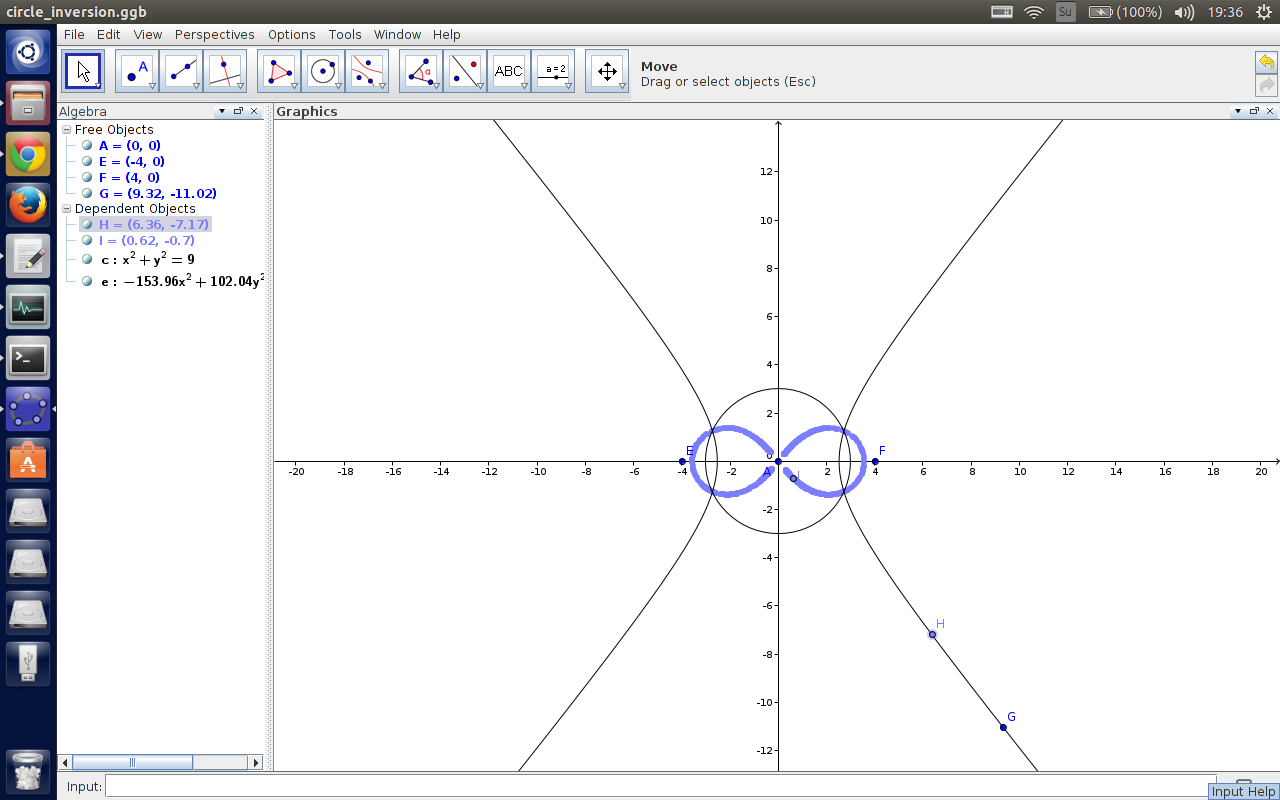
双曲线反演一下变成了 $\infty$...

我们不妨把样例反演一下变成下面这样：

由于反演前后的几何性质是不会发生改变的，比如反演前两个圆相切，反演完以后他们两个还是相切，只不过可能不是圆与圆相切而是直线与圆相切之类的，因此我们可以像这张图这样建立反演中心，圆 $C_1,C_2$ 反演完以后就变成了两条直线，而 $C_3,C_4,\cdots$ 反演完之后，由于没过反演中心，所以还是圆；又因为它们都与圆 $C_1,C_2$ 相切，所以反演以后的圆统统都被夹在了两条直线里面，大小都一样，而且一个挨着一个。

这里详细讲了怎么求一个圆的反演

然而我觉得如果不会求的话，可以随便找圆上的三个点，然后把这三个点反一下，然后再以这三个点画个圆就好了，简单粗暴= =

注意不能直接求圆心。原因在上面第二张截屏。

于是这题的解法已经十分明了了：先把 $C_1,C_2$ 反成直线，解三角形解出 $C_3$ 的位置，然后反成小圆，看一下 $C_4$ 塞哪里符合题意，然后就可以 $O(1)$ 求出第 $n$ 个圆反演完以后的圆，直接反回去就好了。