第一次在uoj写blog

事情是这样的：

一年以前我看了白书上的计算几何，然后看到半平面交这一章，然后看完代码感觉这是什么鬼

so，写(chao)了白书上的模版，然后交了BZOJ1007，狂Wa不止，于是从此就没写过半平面交。还有心理阴影

前几周老师叫我们准备整理模板给小朋友们用，然后在列举模板的时候提到了半平面交，学长说这不是跟凸包没差嘛

什么情况？

于是再次翻了翻白书，发现P277下面有一行注释：

    “从学术上讲，凸包的对偶问题很接近半平面交，所以二者算法很接近。”

为什么就可以很接近呢？到底接近在哪里？

我在网络上找了半天只有一篇WC2012的PPT里面有带过这个问题。可能以前有人写过这个问题但是我没找到。。。

BZOJ1007

在平面直角坐标系上有n条直线。输出在y轴的正无穷处能看到哪几条直线。只有1个点被看见不算.

就是求形如n条 $y≥kx+b$ 的半平面的并，答案一定是形如凸包的下凸壳

嗯，其实是这样对偶的：将一条直线的 $(k,b)$ 视为一个点 $(k,b)$ ，然后做凸包的上凸壳

正确性证明如下：

首先先按直线的斜率排序

假设当前栈内有a,b两条直线，要插入直线c

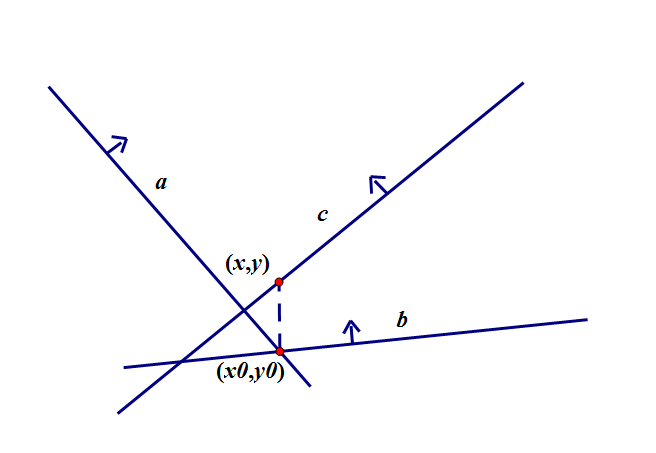
那么，把b踢出栈的充要条件是，a与b的交点在c的下方

假设a与b交于点 $(x_0,y_0)$，那么我们可以列出一个正常求交点来判断的表达式：

即交点 $$(x_0,y_0)=(-\frac{a.b-b.b}{a.k-b.k},\frac{a.k*b.b-a.b*b.k}{a.k-b.k})$$

对于直线c，当$x=x_0$时，带入可得：

由于我们开始的时候按照斜率排序，因此 $a.k > b.k$

所以把b踢出去的条件就是 $y > y_0$，就是这个式子：

好了先把它放在一边

对于这个问题的对偶问题，不妨手画一下，发现踢掉点b的充要条件是，点c在点a、b所构成的直线上方

就是 $cross(B-A,C-A)≥0$

化简一下，惊讶的发现它变成①式了

于是我们成功证明了这两个问题是等价的。什么半平面交，让它都去见凸包吧2333

/**************************************************************
    Problem: 1007
    User: wjy1998
    Language: C++
    Result: Accepted
    Time:72 ms
    Memory:1624 kb
****************************************************************/

#include<cstdio>
#include<algorithm>
#define isd(c) (c>='0'&&c<='9')
char ch,B[1<<15],*S=B,*T=B;
#define getc()(S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++)
int aa,bb;int F(){
    while(ch=getc(),!isd(ch)&&ch!='-');ch=='-'?aa=bb=0:(aa=ch-'0',bb=1);
    while(ch=getc(),isd(ch))aa=aa*10+ch-'0';return bb?aa:-aa;
}
#define N 50010
int n,i,q[N],r;
struct P{int x,y,n;}a[N];
#define PP const P&
bool operator<(PP a,PP b){return a.x<b.x||a.x==b.x&&a.y<b.y;}
P operator-(PP a,PP b){return (P){a.x-b.x,a.y-b.y};}
long long operator*(PP a,PP b){return 1LL*a.x*b.y-1LL*a.y*b.x;}
long long check(PP a,PP b,PP c){return (b-a)*(c-a);}
int main(){
    for(n=F(),i=1;i<=n;i++)a[i]=(P){F(),-F(),i};
    std::sort(a+1,a+1+n);
    for(i=1;i<=n;i++)if(a[i].x!=a[i-1].x){
        while(r>1&&check(a[q[r-1]],a[q[r]],a[i])<=0)r--;q[++r]=i;
    }
    for(i=1;i<=r;i++)q[i]=a[q[i]].n;
    std::sort(q+1,q+1+r);
    for(i=1;i<=r;i++)printf("%d ",q[i]);puts("");
}

解释一下

1. 不是说好的 $(k,b)$ 吗，怎么变成了 $(k,-b)$ ?

其实这样解释更好：

其实就是常量和变量互换，或者说实际上要变成 $(-k,b)$ ?

但是弄成 $(k,-b)$ 的话更符合平时的习惯，这样对偶完以后的凹凸性是一致的，就可以无脑写凸包了233

2. 这是啥意思？

if(a[i].x!=a[i-1].x)....

当两条线k相等时，显然只要b比较大的，b小的直接踢掉。就是一个特判。

3. 为什么跑得这么快？

好像是读入问题，删掉优化后200ms，当然还有机器误差。当然这不是重点

现在我们能用求凸包的方法来求形如 $y≥kx+b$ 的并了，那么如果把大于号改成小于号怎么做？

其实一样的，只要把求上凸壳变成求下凸壳，或者求下凸壳换成求上凸壳就可以了

BZOJ3199

构造特殊的V图(外面有框框)，然后干一些奇怪的事情，支持 $O(n^2)$

一个点所能控制的区域就是所有点与这个点的垂直平分线所构成的半平面交

能不能把这种求“半个”半平面交的方法加以拓展呢？

脑补了半天，好像可以搞

假设它半平面交非空，那么这个半平面必定存在一个上凸壳和一个下凸壳。按照之前的算法，先把直线按照符号分类，搞出来上下凸壳 ( 没按符号分类的话不是直接Wa吗 )

我们只要合并两个凸壳就好了

画一画发现只要删掉头和尾多余的直线，删到不能删为止

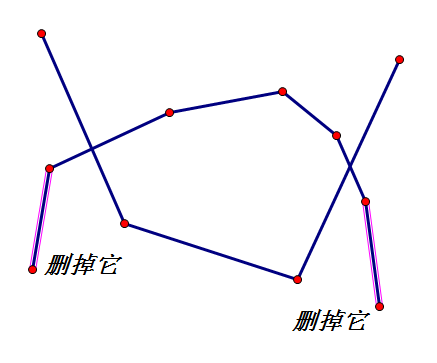
然后就是什么直线求交，分类讨论之类的。可以用bool表达式来简化代码，但是其实没差多少是吧 （对于我这种别人3.6K代码我1.8K的代码的人来说差的就很多了。。。 ）

贴一份具体实现

bool operator<(PP a,PP b){return a.x<b.x||a.x==b.x&&a.y<b.y;}
ld operator&(PP a,PP b){return a.x*b.y-a.y*b.x;}
ld check(PP a,PP b,PP c){return (b-a)&(c-a);}
P calc(PP p,PP v){//y=kx+b
    ld k=v.y/v.x;
    return (P){k,p.y-k*p.x};
}
P getjd(PP a,PP b){//找直线a和b的交点
    ld x=-(b.y-a.y)/(b.x-a.x);
    return (P){x,x*a.x+a.y};
}
#define ck(i) if(tmp.x*a[s].x+tmp.y<a[s].y)b1[++t1]=(P){tmp.x,-tmp.y,i};else b2[++t2]=(P){-tmp.x,tmp.y,i};
void work(int s){//以点s为中心做半平面交
    int i,j,r1=0,r2=0,t1=0,t2=0,l1=1,l2=1,flag;P tmp;
    for(i=1;i<=n;i++)if(i!=s){
        tmp=calc((a[i]+a[s])/2,(a[i]-a[s])*(P){0,1});//复数乘
        ck(i);
    }
    tmp=a0;ck(0);tmp=a1;ck(0);
    tmp=a2;ck(0);tmp=a3;ck(0);
     //a0,a1,a2,a3=大框框
     //下面是做凸包不是做半平面交！！！
    std::sort(b1+1,b1+1+t1);b1[0].x=1e10;
    for(i=1;i<=t1;i++)if(b1[i].x!=b1[i-1].x){
        while(r1>1&&check(b1[q1[r1-1]],b1[q1[r1]],b1[i])<=0)r1--;q1[++r1]=i;
    }
    for(i=1;i<=t1;i++)b1[i].y=-b1[i].y;

    std::sort(b2+1,b2+1+t2);b2[0].x=1e10;
    for(i=1;i<=t2;i++)if(b2[i].x!=b2[i-1].x){
        while(r2>1&&check(b2[q2[r2-1]],b2[q2[r2]],b2[i])<=0)r2--;q2[++r2]=i;
    }
    for(i=1;i<=t2;i++)b2[i].x=-b2[i].x;

    //del_head
    for(;;){flag=0;
        if(l1<r1){
            tmp=getjd(b1[q1[l1]],b1[q1[l1+1]]);
            if(tmp.x*b2[q2[l2]].x+b2[q2[l2]].y<=tmp.y){
                l1++;flag=1;
                continue;
            }
        }
        if(l2<r2){
            tmp=getjd(b2[q2[l2]],b2[q2[l2+1]]);
            if(tmp.x*b1[q1[l1]].x+b1[q1[l1]].y>=tmp.y){
                l2++;flag=1;
                continue;
            }
        }
        if(flag==0)break;
    }
    //del_tail
    for(;;){flag=0;
        if(l1<r1){
            tmp=getjd(b1[q1[r1-1]],b1[q1[r1]]);
            if(tmp.x*b2[q2[r2]].x+b2[q2[r2]].y<=tmp.y){
                r1--;flag=1;
                continue;
            }
        }
        if(l2<r2){
            tmp=getjd(b2[q2[r2-1]],b2[q2[r2]]);
            if(tmp.x*b1[q1[r1]].x+b1[q1[r1]].y>=tmp.y){
                r2--;flag=1;
                continue;
            }
        }
        if(flag==0)break;
    }
    //这里的代码有很多简化的余地，比如把b1[]和b2[]合并成b[2][]，然后用b[i][]和b[i^1][]这样子来搞
    for(i=l1;i<=r1;i++)add(s,b1[q1[i]].n);
    for(i=l2;i<=r2;i++)add(s,b2[q2[i]].n);
}

更进一步

能不能完全替代白书上的传统半平面交？

不知道诶

比如判断半平面交是否为空，先搞出上下凸壳，之后？删除如果跟上面一样的话，如果答案是空集，那么到了最后一条的时候，可行域直接变了

如果不嫌麻烦的话，可以写随机增量法先判掉。

可能还有我脑补不出来的方法

其实这种方法只是细节没那么多，好想好写，精度误差小，好像比传统的写法快233 (详见BZOJ3199status，在不加输入优化的情况下340ms)。最主要的是给大家带来一个不同的思路，根据对偶原理还能干一些其它奇怪的事情

如果哪位神犇有更好的想法的话，欢迎交流~

于是我的第一篇uoj博客就这样结束了