https://www.zhihu.com/question/59156172/answer/168224345

退役正好一年了。把回忆录补完。

肯定有退役的oier很疑惑高三该怎么过。希望能帮到大家。

集训队爷就不用D我这个蒟蒻了qaq

http://trinkle.is-programmer.com/2015/7/21/memory.112423.html

广告：https://pan.baidu.com/s/1o8kyBEE 请各位大爷们免费品尝

或许辛普森积分要成为时代的眼泪了？

格林公式大法好 orzakf

$$\iint_{D}\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=\oint_{C} P dx+Q dy$$ $$let \ P=-y,\ Q=x$$ $$\iint_{D}2 dx dy=\oint_{C} x dy-y dx$$

$Circle(x_0,y_0,r):$

$$\begin{cases}x=x_0+r\cdot cos\theta \\ y=y_0+r\cdot sin\theta\end{cases}$$

设边界端点从$\theta_1$到$\theta_2$（逆时针方向）

$$\begin{eqnarray}S&=&\iint_{D}1 dx dy\\&=&\frac{1}{2}\oint_{C}xdy-ydx\\&=&\frac{1}{2}\int_{\theta_1}^{\theta_2} (x_0+r\cdot cos\theta)d(y_0+r\cdot sin\theta)-(y_0+r\cdot sin\theta)d(x_0+r\cdot cos\theta)\\&=&\frac{r}{2}\int_{\theta_1}^{\theta_2} [(x_0+r\cdot cos\theta)\cdot cos\theta +(y_0+r\cdot sin\theta)\cdot sin\theta ]d\theta\\&=&\frac{r}{2}\int_{\theta_1}^{\theta_2} [x_0\cdot cos\theta + y_0\cdot sin\theta+r]d\theta\\&=&\frac{1}{2}\cdot(f(r,x_0,y_0,\theta_2)-f(r,x_0,y_0,\theta_1))\end{eqnarray}$$

其中

$$f(r,x,y,\theta)=r^2\cdot \theta+r\cdot x\cdot sin\theta-r\cdot y\cdot cos\theta$$

所以对于圆并，只要对于每个圆，求出它在最终图形里面所占的边界，然后加起来就好了

复杂度：$O(n^2\cdot log(n))$

直线也是类似的，式子还比这个更简单

代码比扫描线短了不少2333

BZOJ2178:

/**************************************************************
    Problem: 2178
    User: wjy1998
    Language: C++
    Result: Accepted
    Time:684 ms
    Memory:868 kb
****************************************************************/

#include<cmath>
#include<cstdio>
#include<algorithm>

typedef double ld;

const int N = 1010;
const ld pi = acos(-1);

int n; ld ans;

struct P {
    ld x, y;
    P operator - (const P&a) const {
        return (P) {x - a.x, y - a.y};
    }
    ld len () {
        return sqrt(x * x + y * y);
    }
};

struct C {
    P o; ld r;
    bool operator < (const C&a) const {
        if (o.x != a.o.x) return o.x < a.o.x;
        if (o.y != a.o.y) return o.y < a.o.y;
        return r < a.r;
    }
    bool operator == (const C&a) const {
        return o.x == a.o.x && o.y == a.o.y && r == a.r;
    }
    ld oint (ld t1, ld t2) {
        return r * (r * (t2 - t1) + o.x * (sin(t2) - sin(t1)) - o.y * (cos(t2) - cos(t1)));
    }
} a[N];

struct D {
    ld x; int c;
    bool operator < (const D&a) const {
        return x < a.x;
    }
} pos[N * 2];

ld work (int c) {
    int tot = 0, cnt = 0;
    for (int i = 1; i <= n; i++)
    if (i != c) {
        P d = a[i].o - a[c].o; ld dis = d.len();
        if (a[c].r <= a[i].r - dis) return 0;
        if (a[i].r <= a[c].r - dis || a[i].r + a[c].r <= dis) continue;
        ld g = atan2(d.y, d.x), g0 = acos((dis * dis + a[c].r * a[c].r - a[i].r * a[i].r) / (2 * dis * a[c].r)), l = g - g0, r = g + g0;
        if (l < -pi) l += pi * 2;
        if (r >= pi) r -= pi * 2;
        if (l > r) cnt++;
        pos[++tot] = (D) {l, 1};
        pos[++tot] = (D) {r, -1};
    }
    pos[0].x = -pi, pos[++tot].x = pi;
    std::sort(pos + 1, pos + 1 + tot);
    ld ans = 0;
    for (int i = 1; i <= tot; cnt += pos[i++].c)
        if (cnt == 0) ans += a[c].oint(pos[i - 1].x, pos[i].x);
    return ans;
}

int main () {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%lf%lf%lf",&a[i].o.x, &a[i].o.y, &a[i].r);
    std::sort(a + 1, a + 1 + n);
    n = std::unique(a + 1, a + 1 + n) - a - 1;
    for (int i = 1; i <= n; i++) ans += work(i);
    printf("%.3lf\n", ans / 2);
}

广告：同情一下一只退役多年的高考狗...

戳我

希望能帮到大家

Rank1已经不再重要

新的征程就在前方

Codechef July Challenge 2015 » NTHCIR

虽然我知道在比赛还没结束前挂题解不好，但是还是想骗一发访问量。

题目大概是这样的：

有很多圆，满足 $C_n(n\ge 4)$ 与 $C_1,C_2,\cdots ,C_{n-1}$ 都相切，$C_3$ 与 $C_1,C_2$ 相切，$C_2$ 与 $C_1$ 相切，图形如下：

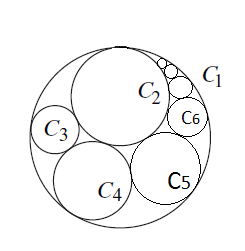
现已知 $r_1,r_2,r_3,r_4$，求 $r_n$。询问数<=1000w，$n\le 10^9$，时限 $1.5s$

例如：当 $r_1=6,r_2=r_3=3,r_4=2$ 的时候，圆大概长这样：

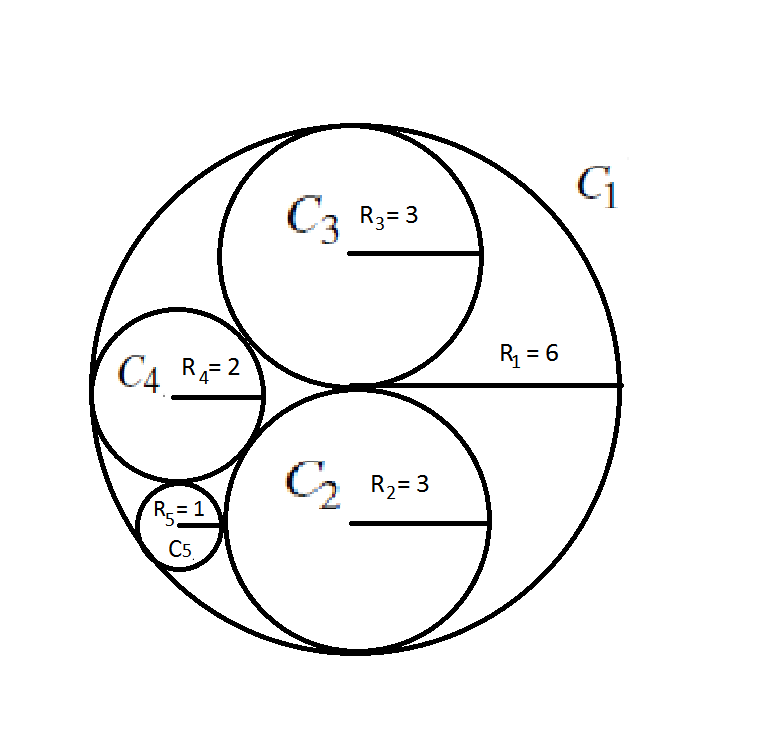
圆的反演是什么呢？

我们先选定一个点 $O$为反演中心，以 $O$ 为圆心，半径为 $r$ 画一个圆。然后对于平面上的点 $P$ 和 $P'$，如果 $P$ 和 $P'$ 在以 $O$ 为起点的射线上，并且 $|OP|\cdot|OP'|=r^2$，那么就说 $P$ 和 $P'$ 互为反演点。

所以圆外的点反演一下会到圆内，圆内会到圆外，圆上则不变。

我找了 $GeoGebra$ 来玩玩，效果差不多是长下面这个样子的：

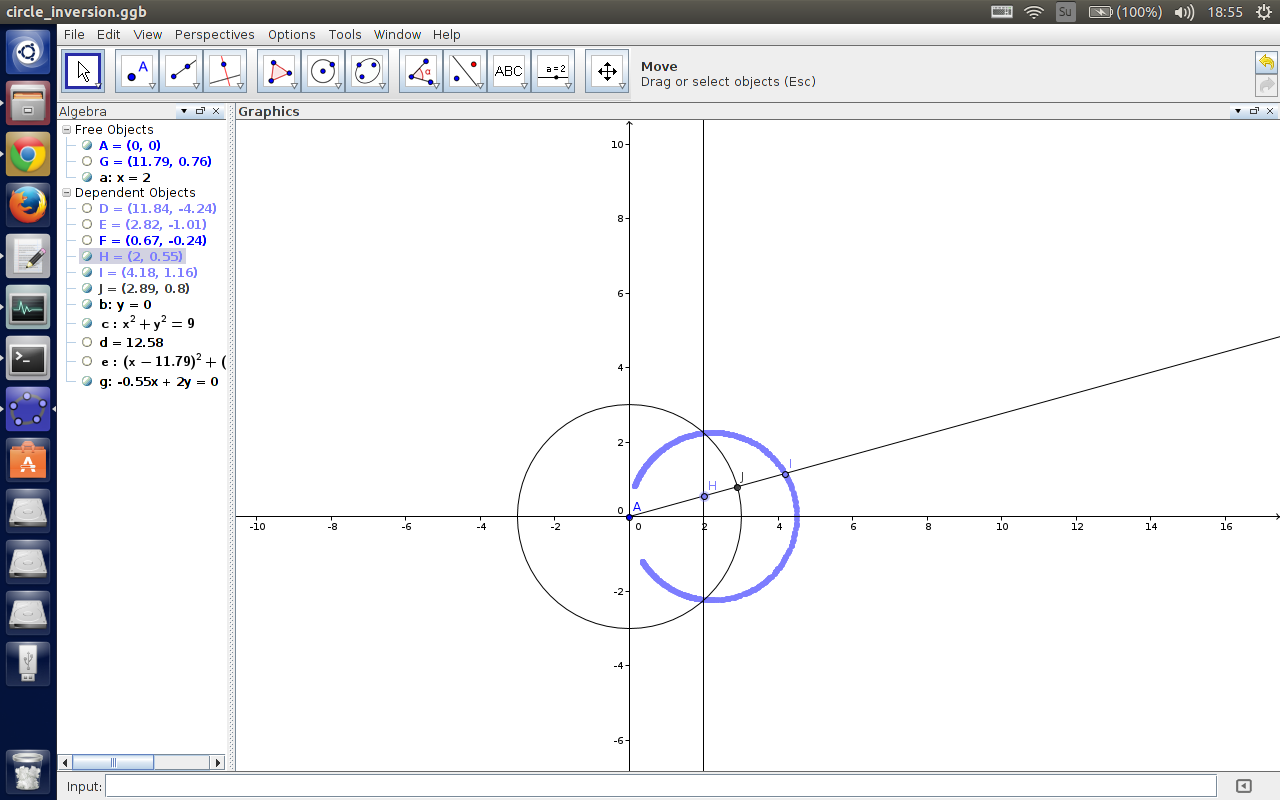
反演中心为坐标原点，点 $H$ 在直线上移动，点 $J$ 为射线 $AH$的焦点，点 $I$ 为点 $H$ 的反演点。

可以看到，一条不过反演中心的直线反演之后变成了一个过反演中心的圆。而且直线和两个圆两两相交。

由于反演的可逆性，这个圆反演一下就变成了一条直线啦~

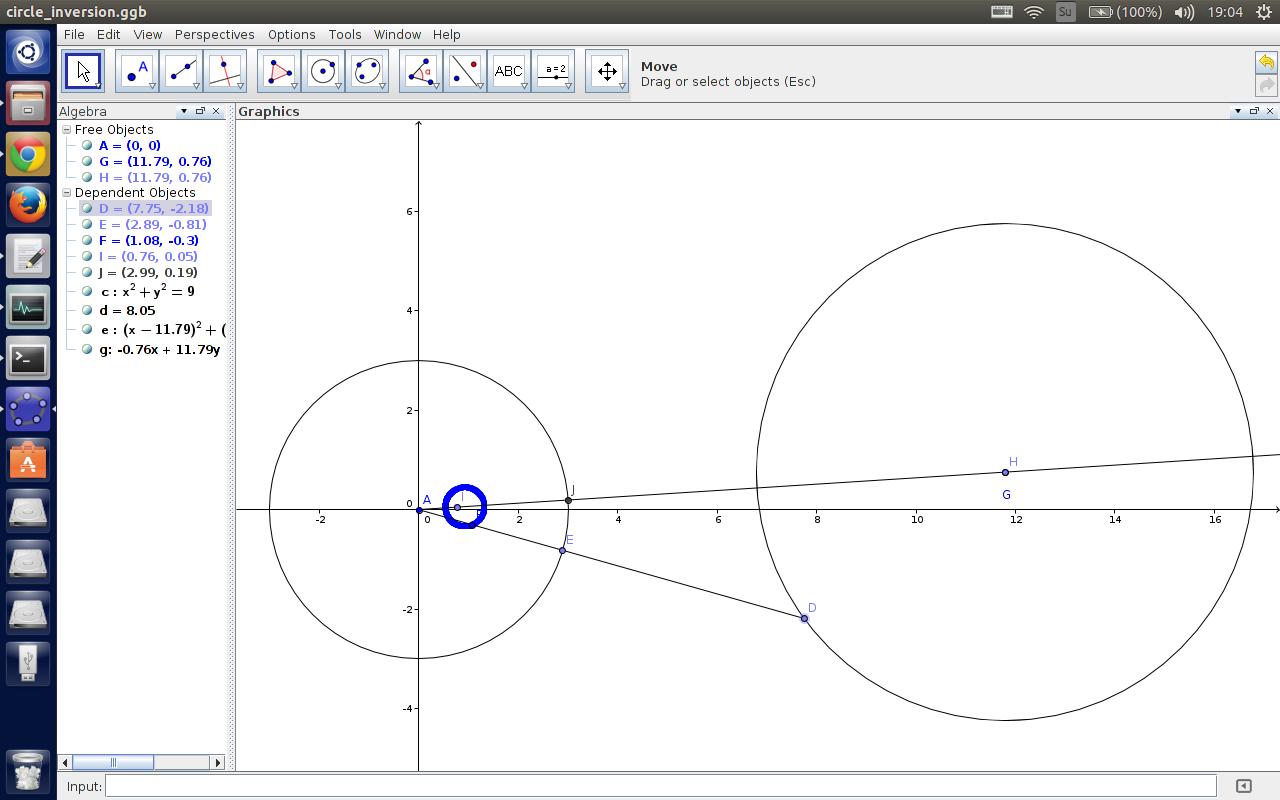
一个不过反演中心的圆反演以后是一个以反演中心位似的圆。

从上面的图来看，显然两个圆是反过来对应的，并不是直接位似。还有切记，圆心反演完以后并不是反演完的圆的圆心，比如上面的点 $H$ 和 $I$。

再来一个好玩点的：

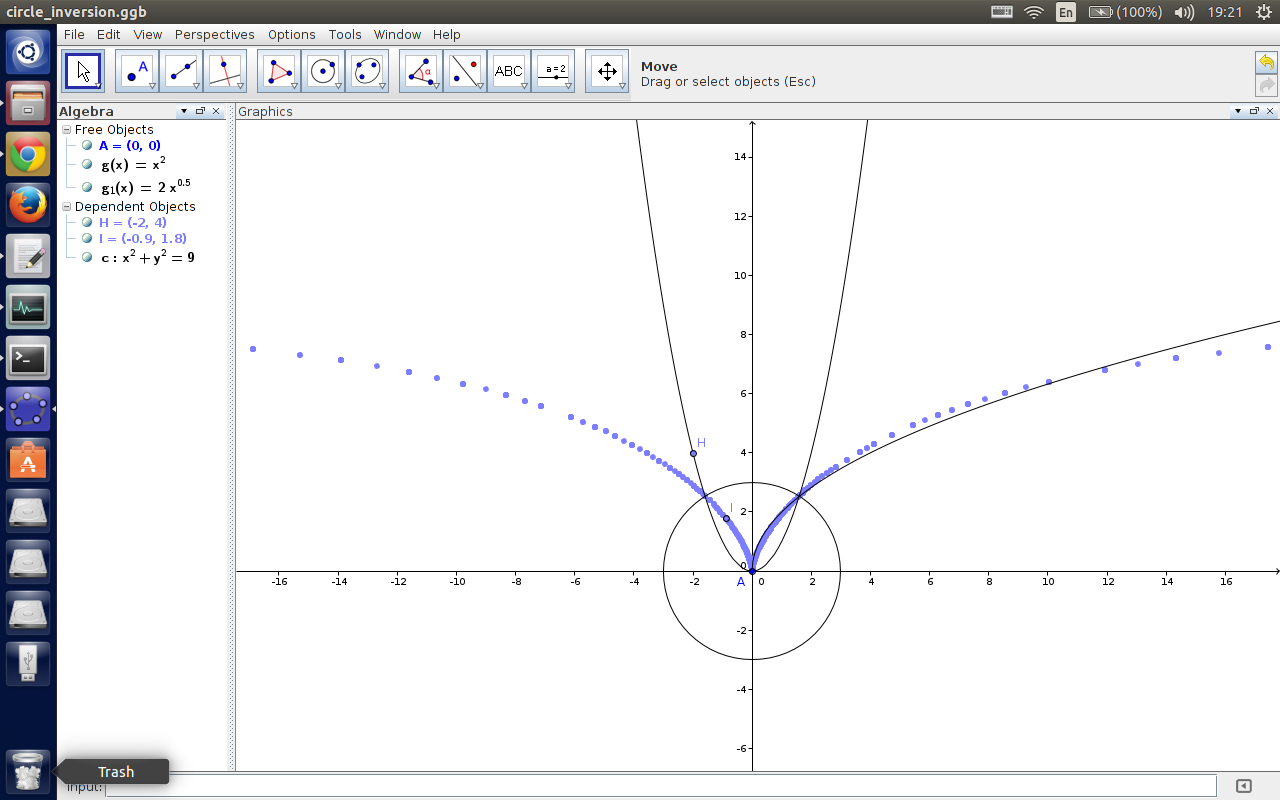
抛物线反演一下，不知道变成了什么。。。右边的黑线是 $2\sqrt{x}$，然而不能拟合。

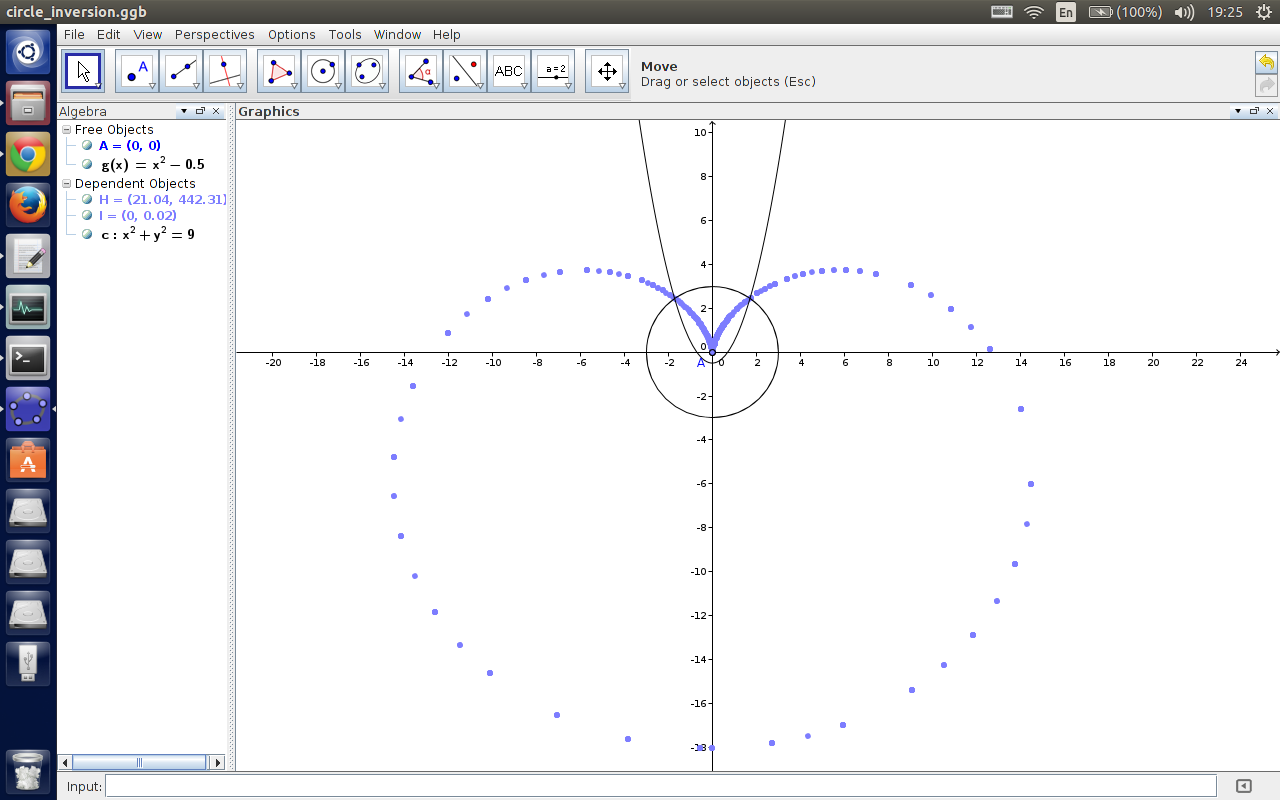
然后稍微往下移一点就变成了心型线！

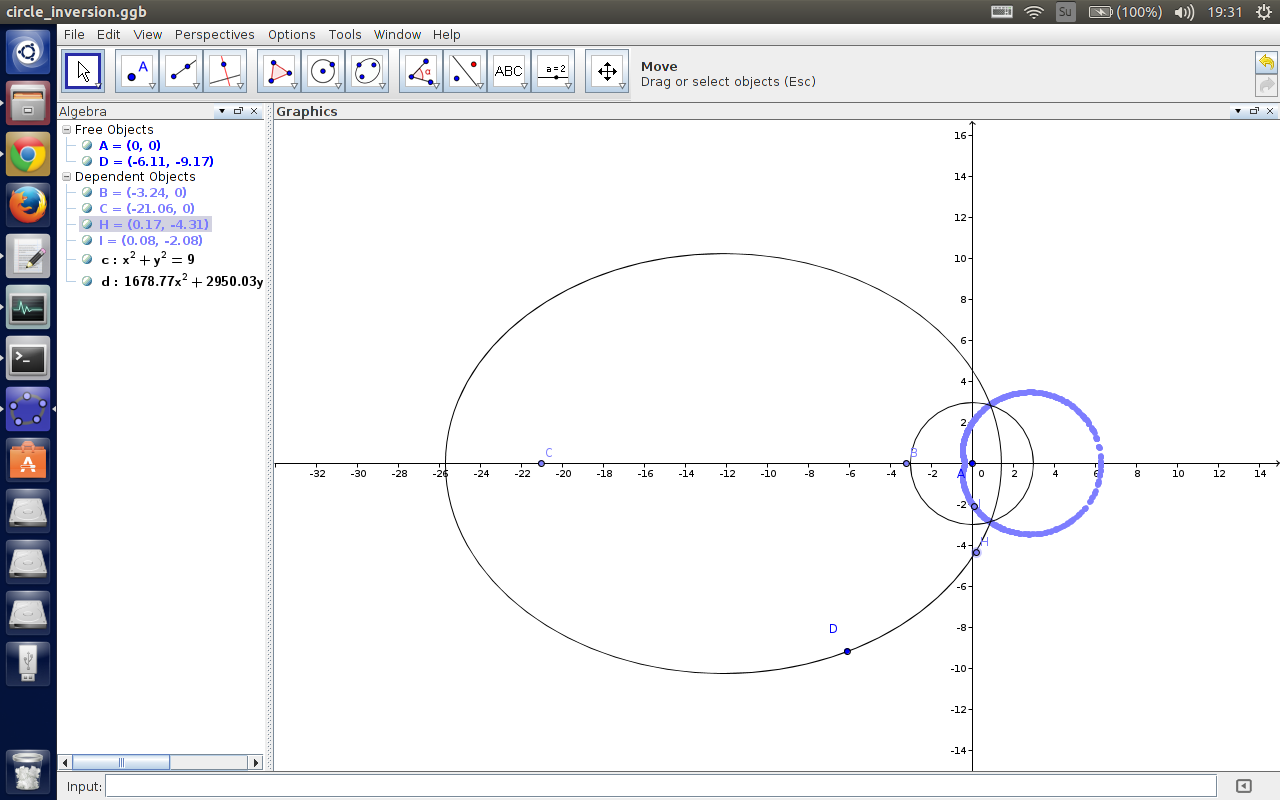
椭圆好像跟上面两种差不多，不是太好玩。

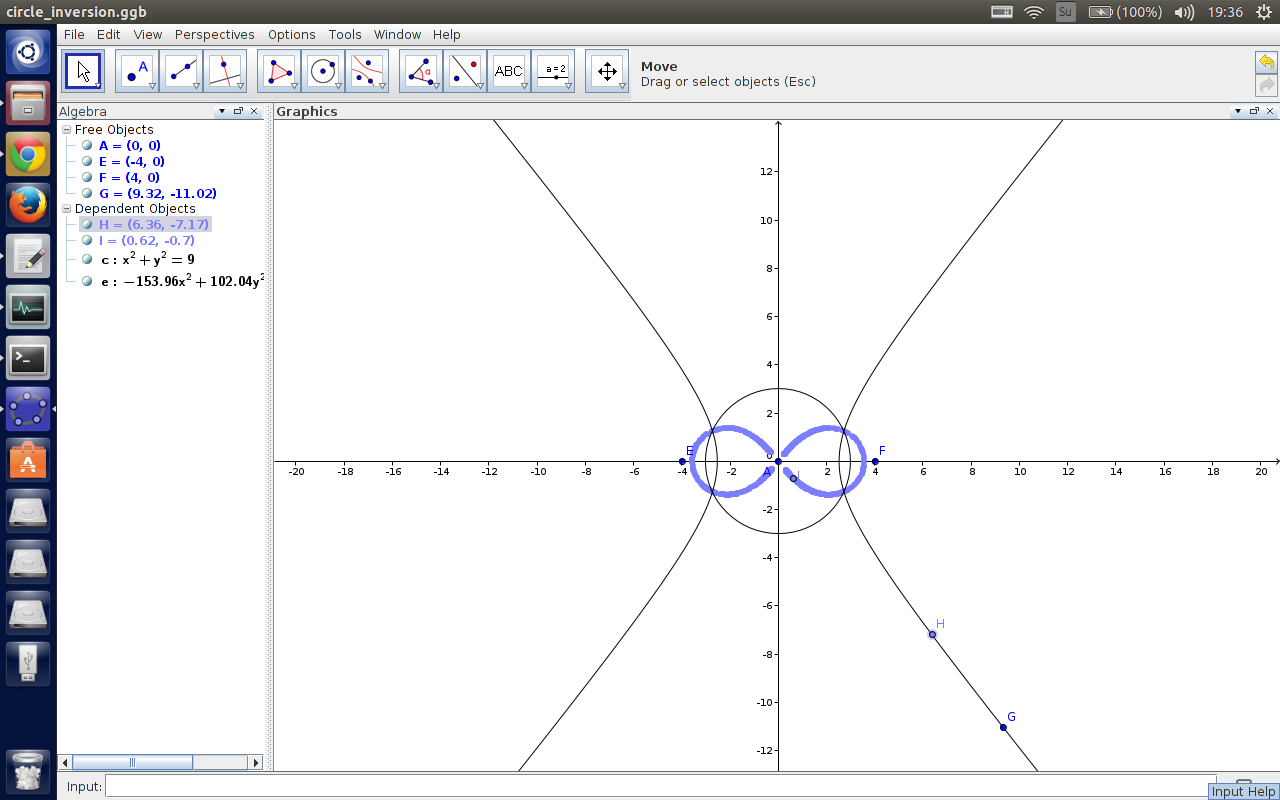
双曲线反演一下变成了 $\infty$...

我们不妨把样例反演一下变成下面这样：

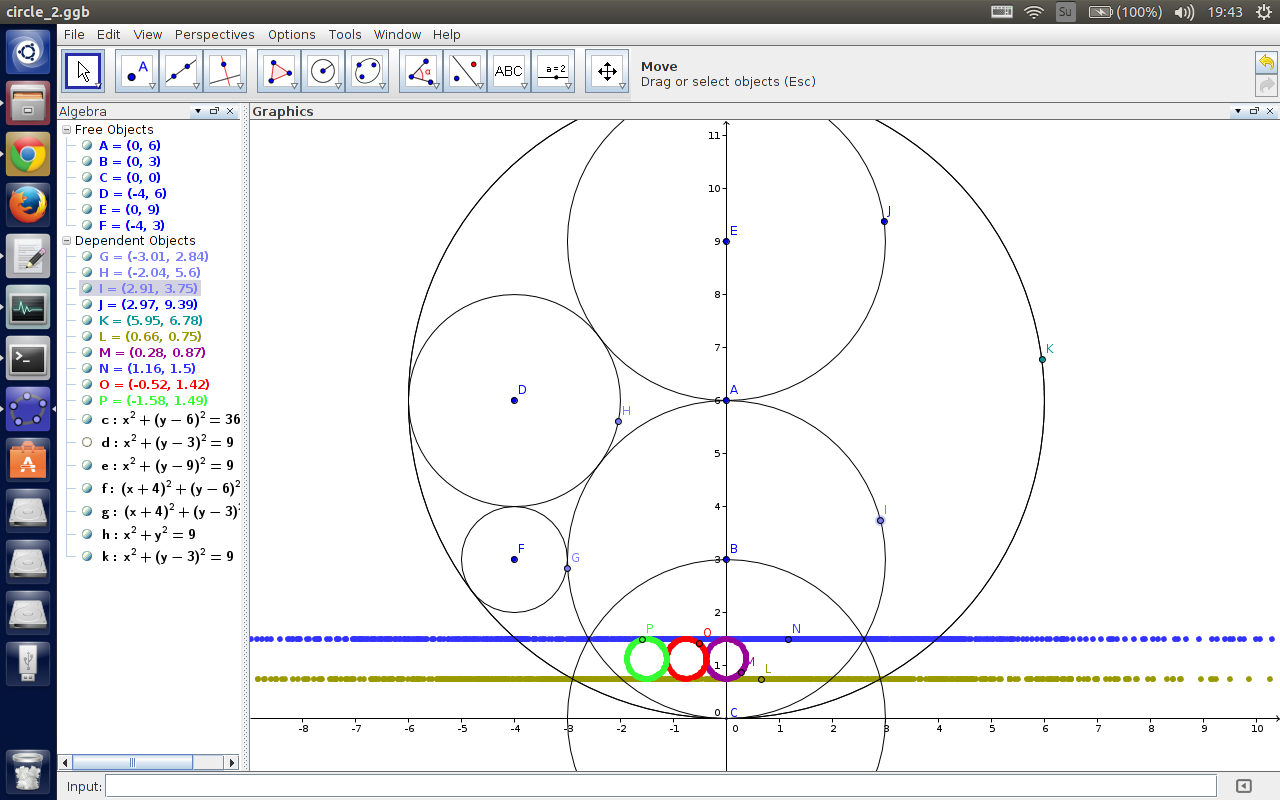
由于反演前后的几何性质是不会发生改变的，比如反演前两个圆相切，反演完以后他们两个还是相切，只不过可能不是圆与圆相切而是直线与圆相切之类的，因此我们可以像这张图这样建立反演中心，圆 $C_1,C_2$ 反演完以后就变成了两条直线，而 $C_3,C_4,\cdots$ 反演完之后，由于没过反演中心，所以还是圆；又因为它们都与圆 $C_1,C_2$ 相切，所以反演以后的圆统统都被夹在了两条直线里面，大小都一样，而且一个挨着一个。

这里详细讲了怎么求一个圆的反演

然而我觉得如果不会求的话，可以随便找圆上的三个点，然后把这三个点反一下，然后再以这三个点画个圆就好了，简单粗暴= =

注意不能直接求圆心。原因在上面第二张截屏。

于是这题的解法已经十分明了了：先把 $C_1,C_2$ 反成直线，解三角形解出 $C_3$ 的位置，然后反成小圆，看一下 $C_4$ 塞哪里符合题意，然后就可以 $O(1)$ 求出第 $n$ 个圆反演完以后的圆，直接反回去就好了。

本题按时间复杂度的不同共有三种解法。

Sol-1 $O(m^2log(n))$

令 $f(n,k)=\sum_{i=1}^n i^k \cdot m^i$

\begin{eqnarray} f(n+1,k)&=&\sum_{i=1}^{n+1} i^k \cdot m^i\\ &=&m+\sum_{i=2}^{n+1} i^k\cdot m^i \\ &=&m+m\sum_{i=1}^n (i+1)^k\cdot m^i \\ &=&m+m\sum_{i=1}^n \sum_{j=0}^k C_k^j\cdot i^j\cdot m^i \\ &=&m+m\sum_{j=0}^k C_k^j\cdot\sum_{i=1}^n i^j\cdot m^i \\ &=&m+m\sum_{j=0}^k C_k^j\cdot f(n,j) \\ \end{eqnarray}

\begin{eqnarray} f(2n,k)&=&\sum_{i=1}^{2n} i^k\cdot m^i\\ &=&\sum_{i=1}^n i^k\cdot m^i +\sum_{i=n+1}^{2n} i^k\cdot m^i\\ &=&f(n,k)+\sum_{i=1}^n (i+n)^k\cdot m^{i+n}\\ &=&f(n,k)+m^n\sum_{i=1}^n m^i\cdot\sum_{j=0}^k C_k^j\cdot i^j\cdot n^{k-j} \\ &=&f(n,k)+m^n\sum_{j=0}^k C_k^j\cdot n^{k-j}\cdot\sum_{i=1}^n i^j\cdot m^i\\ &=&f(n,k)+m^n\sum_{j=0}^k C_k^j\cdot n^{k-j}\cdot f(n,j)\\ \end{eqnarray}

所以我们只要花$O(m^2)$的时间就能从$n$转移到$n+1$或者$2n$，类似快速幂的思想就能在$O(m^2log(n))$的时间内解决这题。

Sol-2 $O(m^2)$

好像网络上的题解都是这个复杂度。

令 $f(k)=\sum_{i=1}^n i^k \cdot m^i$

\begin{eqnarray} (m-1)\cdot f(k)&=&\sum_{i=1}^n i^k\cdot m^{i+1}-\sum_{i=1}^n i^k\cdot m^i \\ &=&\sum_{i=2}^{n+1} (i-1)^k\cdot m^i -\sum_{i=1}^n i^k\cdot m^i \\ &=&n^k\cdot m^{n+1}+\sum_{i=1}^n m^i\cdot[(i-1)^k-i^k]\\ &=&n^k\cdot m^{n+1}+\sum_{i=1}^n m^i\cdot\sum_{j=0}^{k-1}C_k^j\cdot i^j\cdot (-1)^{k-j}\\ &=&n^k\cdot m^{n+1}+\sum_{j=0}^{k-1} C_k^j\cdot (-1)^{k-j}\cdot\sum_{i=1}^n i^j\cdot m^i\\ &=&n^k\cdot m^{n+1}+\sum_{j=0}^{k-1} C_k^j\cdot (-1)^{k-j}\cdot f(j)\\ f(k)&=&\frac{n^k\cdot m^{n+1}+\sum_{j=0}^{k-1} C_k^j\cdot (-1)^{k-j}\cdot f(j)}{m-1}\\ \end{eqnarray} 特判$m=1$的情况，当$m\ne 1$时直接用上面的式子$O(m^2)$转移。

Sol-3 $O(m)$

Orz完杜教的ppt才懂

令$G(n)=\sum_{i=0}^{n-1} i^m\cdot m^i$，注意这里只加到$n-1$

然后把$m$很小的时候的公式找出来：

\begin{eqnarray} m=2&\ \ G(n)=&2^n\cdot (n^2-4\cdot n+6)-6\\ m=3&\ \ G(n)=&3^n\cdot (\frac{4\cdot n^3-18\cdot n^2+36\cdot n-33}{8})+\frac{33}{8}\\ m=4&\ \ G(n)=&4^n\cdot (\frac{27\cdot n^4-144\cdot n^3+360\cdot n^2-528\cdot n+380}{81})-\frac{380}{81}\\ m=5&\ \ G(n)=&5^n\cdot (\frac{128\cdot n^5-800\cdot n^4+2400\cdot n^3-4600\cdot n^2+5700\cdot n-3535}{512})+\frac{3535}{512}\\ m=6&\ \ G(n)=&6^n\cdot (\frac{3125\cdot n^6-22500\cdot n^5+78750\cdot n^4-183000\cdot n^3+305550\cdot n^2-340020\cdot n+189714}{10625})-\frac{189714}{15625}\\ \end{eqnarray}

//公式最后一项的有理数还是一个神奇的数列

根据上面这些公式，不难得出答案的式子一定是长这样的：

$$G(n)=m^n\cdot F_m(n) - F_m(0)$$

其中$F_m(n)$是一个m次多项式(代入$n$后的值)，形如$c_0\cdot n^m + c_1\cdot n^{m-1} + ... + c_{m-1}\cdot n+c_m$

归纳法证一下发现结论是对的。

所以

$$G(n+1)-G(n)=n^m\cdot m^n =m^{n+1}\cdot F_m(n+1)-m^n \cdot F_m(n)$$ $$n^m=m\cdot F_m(n+1)-F_m(n)$$ $$F_m(n+1)=\frac{n^m+F_m(n)}{m}$$

设$F_m(0)=x$，则$F_m(1)$~$F_m(m+1)$都能通过上面的递推式变成形如$Ax+B$的形式。

由于$F_m(n)$是一个次数为$m$的多项式(代入$n$后的值)，所以有下面这个式子：

$$\sum_{i=0}^{m+1} (-1)^i \cdot C_{m+1}^i F_m(i) =0$$

为什么呢？

首先，$F_m(i)$是可以线性表示成若干个组合数之和，于是我们只要证明

$$\forall k\le m, \sum_{i=0}^{m+1} (-1)^i \cdot C_{m+1}^i C_i^k =0$$

注意到$i$的范围只能是$[k,m+1]$，否则后面那坨东西直接变成0。

\begin{eqnarray} &&\sum_{i=k}^{m+1} (-1)^i \cdot C_{m+1}^i \cdot C_i^k\\ &=&\sum_{i=k}^{m+1} (-1)^i \cdot \frac{(m+1)!}{i!\cdot (m+1-i)!}\cdot\frac{i!}{k!\cdot (i-k)!}\\ &=&\frac{(m+1)!}{(m+1-k)!\cdot k!}\sum_{i=k}^{m+1} (-1)^i \cdot \frac{(m+1-k)!}{(m+1-i)!\cdot (i-k)!}\\ &=&C_{m+1}^k \sum_{i=k}^{m+1} (-1)^i \cdot C_{m+1-k}^{i-k}\\ &=&C_{m+1}^k \sum_{i=0}^{m+1-k} (-1)^{i-k}\cdot C_{m+1-k}^i\\ &=&(-1)^k\cdot C_{m+1}^k \cdot (1-1)^{m+1-k}=0\\ \end{eqnarray}

于是这个鬼畜的结论就证完啦~对任意$m$次多项式都能用~

然后就能根据这个式子列方程，就能把$F_m(0)$给解出来。

然而题目不是叫你求$F_m(0)$，而是求$m^n\cdot F_m(n)-F_m(0)$

当$n\le m$的时候，好办，把之前用到的$F_m(n)=A(n)\cdot F_m(0) + B(n)$直接算一下，然后就能得到答案了。

当$n\gt m$的时候，？

假设我们已经求出了$F_m(0),F_m(1),...,F_m(m)$

令$$F_m(n)=\sum_{k=0}^m C_n^k a_k$$

经过二项式反演可得$$a_k=\sum_{j=0}^k (-1)^{k-j}\cdot C_k^j \cdot F_m(j)$$

\begin{eqnarray} F_m(n)&=&\sum_{k=0}^m C_n^k \sum_{j=0}^k (-1)^{k-j}\cdot C_k^j \cdot F_m(j)\\ &=&\sum_{j=0}^m F_m(j)\cdot \sum_{k=j}^m (-1)^{k-j}\cdot C_n^k\cdot C_k^j\\ &=&\sum_{j=0}^m F_m(j)\cdot \sum_{k=j}^m (-1)^{k-j}\cdot \frac{n!\cdot k!}{k!\cdot (n-k)!\cdot j!\cdot (k-j)!}\\ &=&\sum_{j=0}^m F_m(j)\cdot \sum_{k=j}^m (-1)^{k-j}\cdot \frac{n!\cdot (n-j)!}{(n-k)!\cdot j!\cdot (k-j)!\cdot (n-j)!}\\ &=&\sum_{j=0}^m F_m(j)\cdot \sum_{k=j}^m (-1)^{k-j}\cdot C_n^j\cdot C_{n-j}^{k-j}\\ &=&\sum_{j=0}^m F_m(j)\cdot C_n^j \cdot \sum_{k=0}^{m-j} (-1)^k\cdot C_{n-j}^k\\ &=&\sum_{j=0}^m F_m(j)\cdot C_n^j \cdot (-1)^{m-j}\cdot C_{n-j-1}^{m-j}\\ &=&\sum_{j=0}^m F_m(j)\cdot (-1)^{m-j} \cdot \frac{n!\cdot (n-j-1)!}{j!\cdot (n-j)!\cdot (m-j)!\cdot (n-m-1)!}\\ &=&\frac{n!}{(n-m-1)!}\sum_{j=0}^m F_m(j)\cdot (-1)^{m-j}\cdot \frac{1}{j!\cdot (m-j)!\cdot (n-j)}\\ &=&\sum_{j=0}^m F_m(j)\cdot (-1)^{m-j} \cdot \frac{n\cdot (n-1)\cdot ...\cdot (n-m)}{j!\cdot (m-j)!\cdot (n-j)}\\ \end{eqnarray}

$\frac{n\cdot (n-1)\cdot ...\cdot (n-m)}{n-j}$可以用一个前缀乘积和一个后缀乘积优化成$O(m)$的预处理复杂度。

所以只要花$O(m)$的时间就好了。

上面有一步用到了这个式子(第六行到第七行)： \begin{eqnarray} \sum_{i=0}^k (-1)^i \cdot C_n^i &=& C_n^0-C_n^1+...\\ &=&C_{n-1}^0-C_n^1+...\\ &=&-C_{n-1}^1+C_n^2-...\\ &=&C_{n-1}^2-C_n^3+...\\ &=&(-1)^k\cdot C_{n-1}^k\\ \end{eqnarray}

复杂度分析：求$1$~$m+1$的所有阶乘、逆元、阶乘逆元以及$i^m$都能做到$O(m)$的时间复杂度。

求$\forall i \in [1,m] F_m(i)$也只要用线性复杂度。

当$n\le m$的时候，只要用$O(1)$的时间得到答案。

当$n\gt m$的时候，照着最后一个式子求。前面的乘数花$O(m)$的时间算，后面的$\frac{n\cdot (n-1)\cdot ...\cdot (n-m)}{n-j}$,$\frac{1}{j!}$和$\frac{1}{(m-j)!}$直接$O(1)$

打了一个下午题解终于把这个坑给填了233

其实我已经在这篇blog里面贴了代码，然而只有神犇才能看得见。

听说是2015论文题。。。《浅谈字符串匹配的几种方法》例3 在P41

idea来源：KFDong

对于Alice的串先插到AC自动机里面，然后用Bob的串来贡献答案。

考虑什么时候贡献了答案，一个串P能贡献给Sx答案 当且仅当Bob的P串能（沿匹配边或fail边）走到Alice的Sx串终止位置。

所以有一种暴力的做法是，对于新加进来的某个节点，我们暴力沿着这个节点跳fail，如果没更新就更新一下，这样做的复杂度应该可以卡到平方$ n^{4/3}$ 级别。

考虑优化暴力。我上网搜了一下都是一些树链求并的题解，求LCA，dfs序，树状数组，然后T了2333真是喜闻乐见好像论文里就是这种写法。。。

萌萌哒链接君

利用树链的并

将所有要处理的节点按照dfs序排序,然后首先把它们到根的路径+1

随后将相邻两个节点的LCA到根的路径-1

非常科学

怎么加?树链剖分?等TLE吧

只需用树状数组维护DFS序即可

可惜卡常数!

用倍增LCA会超时

于是我们换用RMQlca,并用ZKW线段树维护

估计ST表预处理也会超时

然后Orz了kfdong，发现LCT可以直接上！整个人都惊呆了

我的access代码大概长这样：

void access(int t,int las=0){
    for(;t;splay(t),son[t][1]=las,las=t,t=fa[t]);
}

LCT求LCA：假设求lca(x,y)，那么access(x),access(y)，做完y以后的las就是LCA。

对于这道题而言，我们求出fail树，然后在上面维护两个标记，一个是时间戳，另一个是增量。

不是要把树链并起来吗？还是用access，只不过多访问一次时间戳。如果节点t之前的点已经在这一个时间段更新过了，那么就停止access，然后打标记。这样就可以不用容斥了~

然后写一下交一发，发现跑了8s+（我机子慢一个测试点开了O2要跑24s+。。。。真是一个悲伤的故事）

还有什么地方可以优化的呢？

再次Orz了AKF的代码以后，发现他有一个优化，缩点！将不是danger标记的节点统统删掉，这样的话点集规模直接变成了n，然后剩下的该怎么做就怎么做，一下子跑进了4s

试了试IO，好像数据有问题还是自己写龊了会RE。于是就扔在一边不管了。。。

来来来贴代码

/**************************************************************
    Problem: 3881
    User: wjy1998
    Language: C++
    Result: Accepted
    Time:3496 ms
    Memory:242856 kb
****************************************************************/

#include<cstdio>
#include<algorithm>
#define N 1620000
int n,m,i,j,fail[N],ch[N][26],tot,las,end[N],q[N],danger[N],id[N];char s[N];
int fa[N],son[N][2],add[N],cnt[N],tim[N],vis[N],tc;
#define ls son[t][0]
#define rs son[t][1]
#define nr(t) (son[fa[t]][0]==t||son[fa[t]][1]==t)
void pd(int t){if(!t)return;
    if(add[t]){
        add[ls]+=add[t],add[rs]+=add[t];
        cnt[ls]+=add[t],cnt[rs]+=add[t];add[t]=0;
    }
    if(tim[ls]<tim[t]||vis[ls]<tim[t])vis[ls]=tim[ls]=tim[t];
    if(tim[rs]<tim[t]||vis[rs]<tim[t])vis[rs]=tim[rs]=tim[t];
}
void rtt(int t){
    int f=fa[t],p=son[f][1]==t;
    fa[t]=fa[f],nr(f)?son[fa[f]][son[fa[f]][1]==f]=t:1;
    (son[f][p]=son[t][p^1])?fa[son[f][p]]=f:1,son[fa[f]=t][p^1]=f;
}
void pv(int t){if(nr(t))pv(fa[t]);pd(t);}
void splay(int t){int f;
    for(pv(t);nr(t);rtt(t))
    if(f=fa[t],nr(f))rtt(son[f][1]==t^son[fa[f]][1]==f?t:f);
}
void access(int t){int las=0;
    for(;t&&(splay(t),vis[t]<tc);rs=las,las=t,t=fa[t]);
    if(las&&vis[las]<tc)tim[las]=vis[las]=tc,add[las]++,cnt[las]++,splay(las);
}
void build_AC(){
    int l,r,i,j,cnt=1;
    for(q[l=r=0]=0;l<=r;l++)
    for(i=0;i<26;i++)
    if(j=ch[q[l]][i]){
        if(q[l])fail[j]=ch[fail[q[l]]][i];
        q[++r]=j;
    }
    else ch[q[l]][i]=ch[fail[q[l]]][i];
    for(id[0]=i=1;i<=r;i++)
    if(danger[q[i]]){
        id[q[i]]=++cnt;
        fa[cnt]=id[fail[q[i]]];
    }
    else id[q[i]]=id[fail[q[i]]];
}
int main(){
    scanf("%d\n",&n);
    for(i=1;i<=n;i++){
        scanf("%s",s);
        for(las=j=0;s[j];j++){
            s[j]-='a';
            if(!ch[las][s[j]])ch[las][s[j]]=++tot;
            las=ch[las][s[j]];
        }
        end[i]=las;danger[las]=1;
    }
    build_AC();
    for(scanf("%d",&m);m--;){
        scanf("%s",s);
        if(s[0]=='1'){
            scanf("%s",s);tc++;
            for(las=i=0;s[i];i++){
                las=ch[las][s[i]-'a'];
                access(id[las]);
            }
        }
        else{
            scanf("%d",&i);i=id[end[i]];
            pv(i);printf("%d\n",cnt[i]);
        }
    }
}

我并没写过树链剖分但是想想 好像不能用在这里？

最后打个广告->戳我...别戳前面那个戳我戳我

//只是自己做个备份

网络上好像没有几篇有介绍这个东西的

首先结构体

struct KDTree{
    int d[2],s[2],x[2],y[2];
}t[N];

d-维度，s-儿子，x-x坐标范围，y-y坐标范围

然后估价，这里的估价是算出下界或上界

距离最小：一个点离当前域的最短距离（内部为0）

距离最大：一个点离当前域端点的最长距离

以平面为例，(x,y)为查询的坐标

曼哈顿最小：

max(t[p].x[0]-x,0)+max(x-t[p].x[1],0)+max(t[p].y[0]-y,0)+max(y-t[p].y[1],0);

曼哈顿最大

max(abs(x-t[p].x[1]),abs(t[p].x[0]-x))+max(abs(y-t[p].y[1]),abs(t[p].y[0]-y));

欧几里德最小

sqr(max(max(x-t[p].x[1],t[p].x[0]-x),0))+sqr(max(max(y-t[p].y[1],t[p].y[0]-y),0))

欧几里德最大

max(sqr(x-t[p].x[0]),sqr(x-t[p].x[1]))+max(sqr(y-t[p].y[0]),sqr(y-t[p].y[1]))

切比雪夫距离？把坐标转45°就是曼哈顿距离了233

我们学校的P1000 A+B problem下面已经有差不多30篇题解了，不知道其他学校的神犇们有没有参与这项活动。。。

挑了几个有意思的抠出来（我只是搬运工= =）

1. 这题可以采用最大流解决。具体做法是在s和t之间加一条流量为a的边和流量为b的边。求该网络的最大流。

2. 这题可用是上下界最小流解决，我们可以由源到汇连2条边，1条下界为a上界无穷大,还有1条下界为b上界也为无穷大，之后套个最小流的模板即可AC

3. 本题属于网络流类型。但这里有个既快又方便的算法：随机加法！随机给出一个整数，判断是否为a+b的值，如果是则输出。时间复杂度：O(1)-O(2*maxlongint)。

4. 这题可以转化为一种经典的统计问题求解。在[-Maxlongint,Maxlongint]范围内求x满足x=a+b输出每一个符合条件的x

5. 本题初看困难，但可以把它看成一道图论最短路模型，设图中有3个点 1 到 2号点有一条长为a的连边 2到3有一条长为b的边 1到3有一条长为maxint的边 求1到3的最短路

6. 一眼看过去这题可能对新手有点难，但只要你知道了树状数组，本题可以转化为树状数组来解决。先用树状数组维护一个所有位均为1的序列。a+b的值即为1~a的和加上1~b的和，这个求和我们就可以使用树状数组的求和搞定，即使是动态数据，我们有了动态求和的利器树状数组，对于m组询问，就可以在O(100000lg(100000) + m(lg(a)+lg(b)))的时间里对每组数据求解，代码又简短！

7. 这题其实是裸的插头DP。我们构造一个2*2的网格，网格第1行第1列的数是a，第2行第2列的数是b，其他数是0。那么问题就变成求代价最小的哈密尔顿回路了。

8. 这题其实是裸的FFT，考虑(1+a)*(1+b)=1+a+b+ab，所以乘完以后第一项就是答案。

9. 本题其实是后缀数组的模板题。构造s，前a位为'b'，后b位为'a'，求sa[]和rank[]以及height[]之后，我们惊讶的发现，其实sa[1]就是答案了。。。

10. 其实这是一道费用流裸题，在有向图里有一个点，源到它的流量为1，费用为－a，它到汇的流量为1，费用为－b，然后求最小费用最大流就好了。

11. 这题其实是裸的LCT。假设有4个点，1到2连a，2到3连b，3到4连0，剩下的边连+oo。考虑将边排序，先求MST，然后不断往里面加新边，求出每个状态的MST边权和，最小值即为答案。

第一次在uoj写blog

事情是这样的：

一年以前我看了白书上的计算几何，然后看到半平面交这一章，然后看完代码感觉这是什么鬼

so，写(chao)了白书上的模版，然后交了BZOJ1007，狂Wa不止，于是从此就没写过半平面交。还有心理阴影

前几周老师叫我们准备整理模板给小朋友们用，然后在列举模板的时候提到了半平面交，学长说这不是跟凸包没差嘛

什么情况？

于是再次翻了翻白书，发现P277下面有一行注释：

    “从学术上讲，凸包的对偶问题很接近半平面交，所以二者算法很接近。”

为什么就可以很接近呢？到底接近在哪里？

我在网络上找了半天只有一篇WC2012的PPT里面有带过这个问题。可能以前有人写过这个问题但是我没找到。。。

BZOJ1007

在平面直角坐标系上有n条直线。输出在y轴的正无穷处能看到哪几条直线。只有1个点被看见不算.

就是求形如n条 $y≥kx+b$ 的半平面的并，答案一定是形如凸包的下凸壳

嗯，其实是这样对偶的：将一条直线的 $(k,b)$ 视为一个点 $(k,b)$ ，然后做凸包的上凸壳

正确性证明如下：

首先先按直线的斜率排序

假设当前栈内有a,b两条直线，要插入直线c

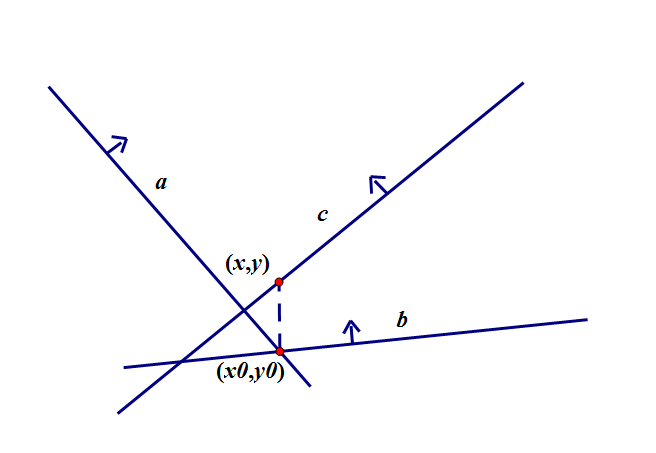
那么，把b踢出栈的充要条件是，a与b的交点在c的下方

假设a与b交于点 $(x_0,y_0)$，那么我们可以列出一个正常求交点来判断的表达式：

即交点 $$(x_0,y_0)=(-\frac{a.b-b.b}{a.k-b.k},\frac{a.k*b.b-a.b*b.k}{a.k-b.k})$$

对于直线c，当$x=x_0$时，带入可得：

由于我们开始的时候按照斜率排序，因此 $a.k > b.k$

所以把b踢出去的条件就是 $y > y_0$，就是这个式子：

好了先把它放在一边

对于这个问题的对偶问题，不妨手画一下，发现踢掉点b的充要条件是，点c在点a、b所构成的直线上方

就是 $cross(B-A,C-A)≥0$

化简一下，惊讶的发现它变成①式了

于是我们成功证明了这两个问题是等价的。什么半平面交，让它都去见凸包吧2333

/**************************************************************
    Problem: 1007
    User: wjy1998
    Language: C++
    Result: Accepted
    Time:72 ms
    Memory:1624 kb
****************************************************************/

#include<cstdio>
#include<algorithm>
#define isd(c) (c>='0'&&c<='9')
char ch,B[1<<15],*S=B,*T=B;
#define getc()(S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++)
int aa,bb;int F(){
    while(ch=getc(),!isd(ch)&&ch!='-');ch=='-'?aa=bb=0:(aa=ch-'0',bb=1);
    while(ch=getc(),isd(ch))aa=aa*10+ch-'0';return bb?aa:-aa;
}
#define N 50010
int n,i,q[N],r;
struct P{int x,y,n;}a[N];
#define PP const P&
bool operator<(PP a,PP b){return a.x<b.x||a.x==b.x&&a.y<b.y;}
P operator-(PP a,PP b){return (P){a.x-b.x,a.y-b.y};}
long long operator*(PP a,PP b){return 1LL*a.x*b.y-1LL*a.y*b.x;}
long long check(PP a,PP b,PP c){return (b-a)*(c-a);}
int main(){
    for(n=F(),i=1;i<=n;i++)a[i]=(P){F(),-F(),i};
    std::sort(a+1,a+1+n);
    for(i=1;i<=n;i++)if(a[i].x!=a[i-1].x){
        while(r>1&&check(a[q[r-1]],a[q[r]],a[i])<=0)r--;q[++r]=i;
    }
    for(i=1;i<=r;i++)q[i]=a[q[i]].n;
    std::sort(q+1,q+1+r);
    for(i=1;i<=r;i++)printf("%d ",q[i]);puts("");
}

解释一下

1. 不是说好的 $(k,b)$ 吗，怎么变成了 $(k,-b)$ ?

其实这样解释更好：

其实就是常量和变量互换，或者说实际上要变成 $(-k,b)$ ?

但是弄成 $(k,-b)$ 的话更符合平时的习惯，这样对偶完以后的凹凸性是一致的，就可以无脑写凸包了233

2. 这是啥意思？

if(a[i].x!=a[i-1].x)....

当两条线k相等时，显然只要b比较大的，b小的直接踢掉。就是一个特判。

3. 为什么跑得这么快？

好像是读入问题，删掉优化后200ms，当然还有机器误差。当然这不是重点

现在我们能用求凸包的方法来求形如 $y≥kx+b$ 的并了，那么如果把大于号改成小于号怎么做？

其实一样的，只要把求上凸壳变成求下凸壳，或者求下凸壳换成求上凸壳就可以了

BZOJ3199

构造特殊的V图(外面有框框)，然后干一些奇怪的事情，支持 $O(n^2)$

一个点所能控制的区域就是所有点与这个点的垂直平分线所构成的半平面交

能不能把这种求“半个”半平面交的方法加以拓展呢？

脑补了半天，好像可以搞

假设它半平面交非空，那么这个半平面必定存在一个上凸壳和一个下凸壳。按照之前的算法，先把直线按照符号分类，搞出来上下凸壳 ( 没按符号分类的话不是直接Wa吗 )

我们只要合并两个凸壳就好了

画一画发现只要删掉头和尾多余的直线，删到不能删为止

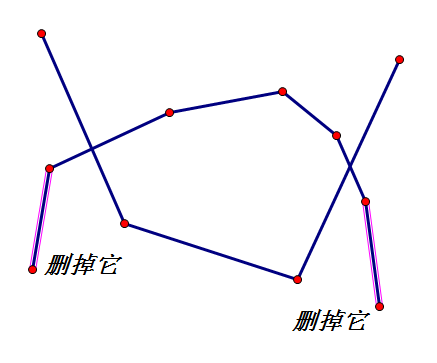
然后就是什么直线求交，分类讨论之类的。可以用bool表达式来简化代码，但是其实没差多少是吧 （对于我这种别人3.6K代码我1.8K的代码的人来说差的就很多了。。。 ）

贴一份具体实现

bool operator<(PP a,PP b){return a.x<b.x||a.x==b.x&&a.y<b.y;}
ld operator&(PP a,PP b){return a.x*b.y-a.y*b.x;}
ld check(PP a,PP b,PP c){return (b-a)&(c-a);}
P calc(PP p,PP v){//y=kx+b
    ld k=v.y/v.x;
    return (P){k,p.y-k*p.x};
}
P getjd(PP a,PP b){//找直线a和b的交点
    ld x=-(b.y-a.y)/(b.x-a.x);
    return (P){x,x*a.x+a.y};
}
#define ck(i) if(tmp.x*a[s].x+tmp.y<a[s].y)b1[++t1]=(P){tmp.x,-tmp.y,i};else b2[++t2]=(P){-tmp.x,tmp.y,i};
void work(int s){//以点s为中心做半平面交
    int i,j,r1=0,r2=0,t1=0,t2=0,l1=1,l2=1,flag;P tmp;
    for(i=1;i<=n;i++)if(i!=s){
        tmp=calc((a[i]+a[s])/2,(a[i]-a[s])*(P){0,1});//复数乘
        ck(i);
    }
    tmp=a0;ck(0);tmp=a1;ck(0);
    tmp=a2;ck(0);tmp=a3;ck(0);
     //a0,a1,a2,a3=大框框
     //下面是做凸包不是做半平面交！！！
    std::sort(b1+1,b1+1+t1);b1[0].x=1e10;
    for(i=1;i<=t1;i++)if(b1[i].x!=b1[i-1].x){
        while(r1>1&&check(b1[q1[r1-1]],b1[q1[r1]],b1[i])<=0)r1--;q1[++r1]=i;
    }
    for(i=1;i<=t1;i++)b1[i].y=-b1[i].y;

    std::sort(b2+1,b2+1+t2);b2[0].x=1e10;
    for(i=1;i<=t2;i++)if(b2[i].x!=b2[i-1].x){
        while(r2>1&&check(b2[q2[r2-1]],b2[q2[r2]],b2[i])<=0)r2--;q2[++r2]=i;
    }
    for(i=1;i<=t2;i++)b2[i].x=-b2[i].x;

    //del_head
    for(;;){flag=0;
        if(l1<r1){
            tmp=getjd(b1[q1[l1]],b1[q1[l1+1]]);
            if(tmp.x*b2[q2[l2]].x+b2[q2[l2]].y<=tmp.y){
                l1++;flag=1;
                continue;
            }
        }
        if(l2<r2){
            tmp=getjd(b2[q2[l2]],b2[q2[l2+1]]);
            if(tmp.x*b1[q1[l1]].x+b1[q1[l1]].y>=tmp.y){
                l2++;flag=1;
                continue;
            }
        }
        if(flag==0)break;
    }
    //del_tail
    for(;;){flag=0;
        if(l1<r1){
            tmp=getjd(b1[q1[r1-1]],b1[q1[r1]]);
            if(tmp.x*b2[q2[r2]].x+b2[q2[r2]].y<=tmp.y){
                r1--;flag=1;
                continue;
            }
        }
        if(l2<r2){
            tmp=getjd(b2[q2[r2-1]],b2[q2[r2]]);
            if(tmp.x*b1[q1[r1]].x+b1[q1[r1]].y>=tmp.y){
                r2--;flag=1;
                continue;
            }
        }
        if(flag==0)break;
    }
    //这里的代码有很多简化的余地，比如把b1[]和b2[]合并成b[2][]，然后用b[i][]和b[i^1][]这样子来搞
    for(i=l1;i<=r1;i++)add(s,b1[q1[i]].n);
    for(i=l2;i<=r2;i++)add(s,b2[q2[i]].n);
}

更进一步

能不能完全替代白书上的传统半平面交？

不知道诶

比如判断半平面交是否为空，先搞出上下凸壳，之后？删除如果跟上面一样的话，如果答案是空集，那么到了最后一条的时候，可行域直接变了

如果不嫌麻烦的话，可以写随机增量法先判掉。

可能还有我脑补不出来的方法

其实这种方法只是细节没那么多，好想好写，精度误差小，好像比传统的写法快233 (详见BZOJ3199status，在不加输入优化的情况下340ms)。最主要的是给大家带来一个不同的思路，根据对偶原理还能干一些其它奇怪的事情

如果哪位神犇有更好的想法的话，欢迎交流~

于是我的第一篇uoj博客就这样结束了