Codechef July Challenge 2015 » NTHCIR

虽然我知道在比赛还没结束前挂题解不好，但是还是想骗一发访问量。

题目大概是这样的：

有很多圆，满足 $C_n(n\ge 4)$ 与 $C_1,C_2,\cdots ,C_{n-1}$ 都相切，$C_3$ 与 $C_1,C_2$ 相切，$C_2$ 与 $C_1$ 相切，图形如下：

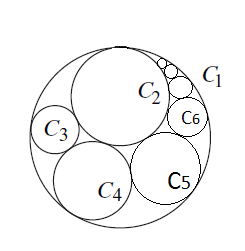
现已知 $r_1,r_2,r_3,r_4$，求 $r_n$。询问数<=1000w，$n\le 10^9$，时限 $1.5s$

例如：当 $r_1=6,r_2=r_3=3,r_4=2$ 的时候，圆大概长这样：

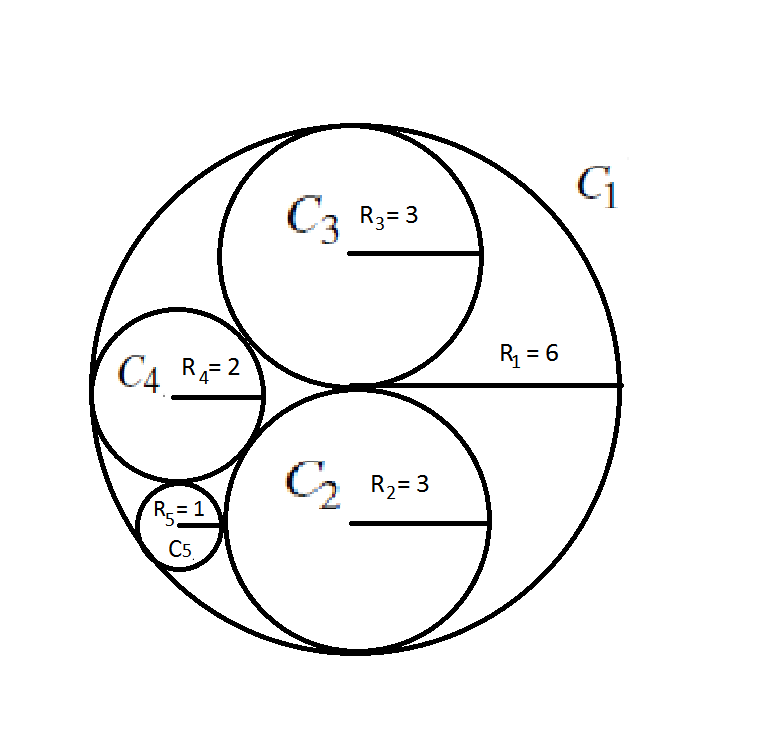
圆的反演是什么呢？

我们先选定一个点 $O$为反演中心，以 $O$ 为圆心，半径为 $r$ 画一个圆。然后对于平面上的点 $P$ 和 $P'$，如果 $P$ 和 $P'$ 在以 $O$ 为起点的射线上，并且 $|OP|\cdot|OP'|=r^2$，那么就说 $P$ 和 $P'$ 互为反演点。

所以圆外的点反演一下会到圆内，圆内会到圆外，圆上则不变。

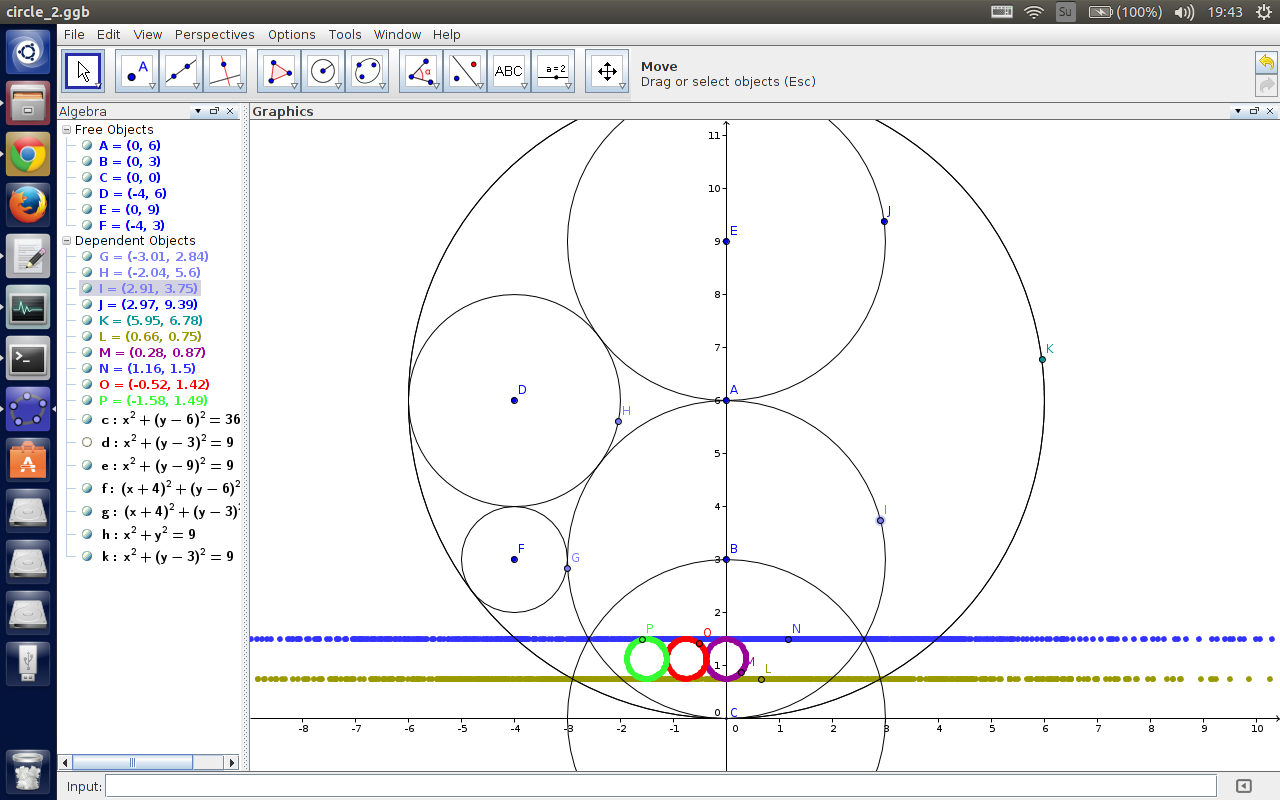
我找了 $GeoGebra$ 来玩玩，效果差不多是长下面这个样子的：

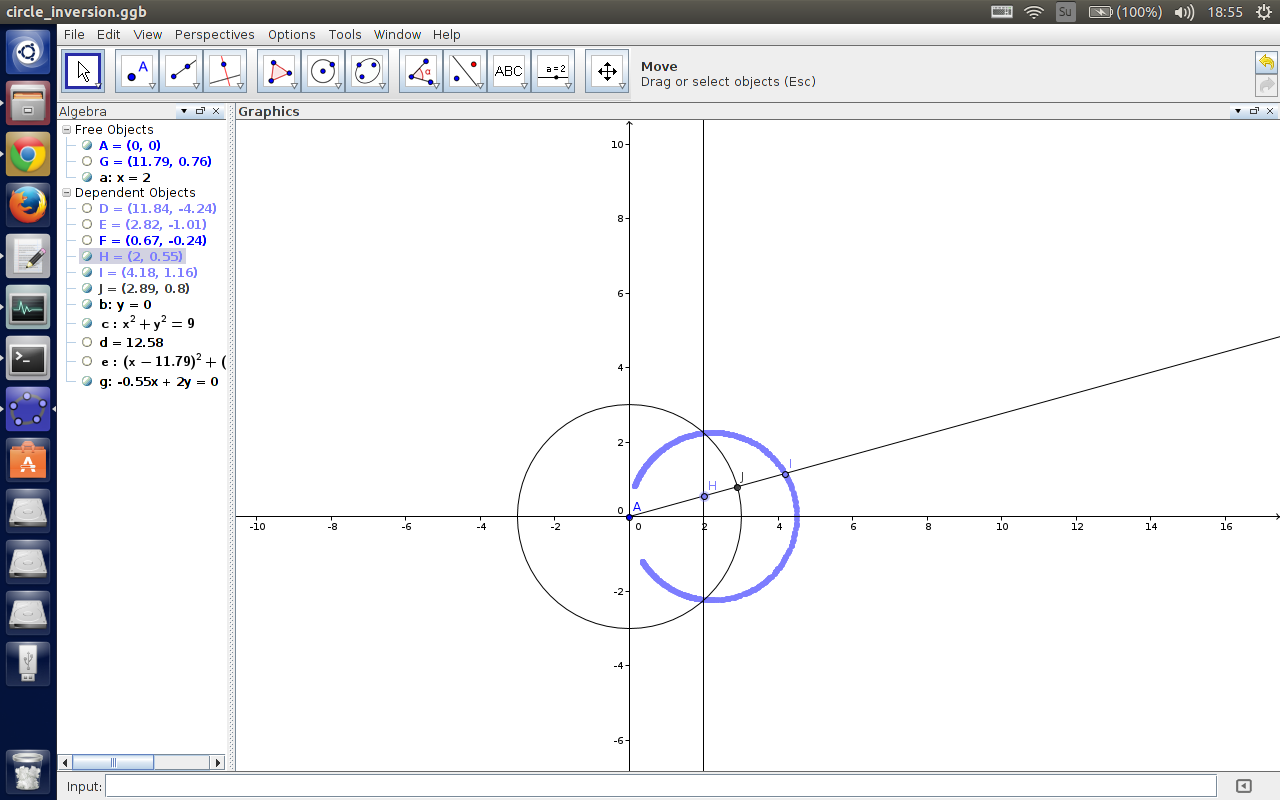
反演中心为坐标原点，点 $H$ 在直线上移动，点 $J$ 为射线 $AH$的焦点，点 $I$ 为点 $H$ 的反演点。

可以看到，一条不过反演中心的直线反演之后变成了一个过反演中心的圆。而且直线和两个圆两两相交。

由于反演的可逆性，这个圆反演一下就变成了一条直线啦~

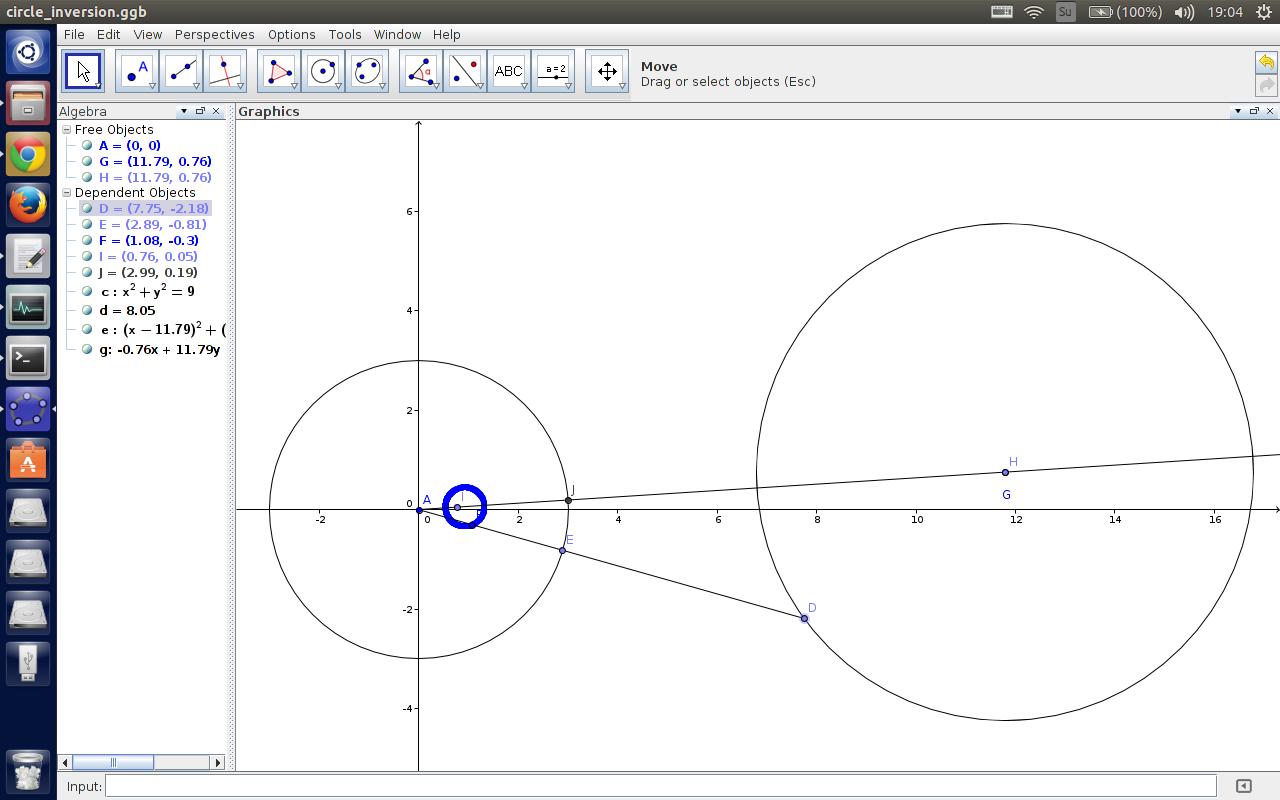
一个不过反演中心的圆反演以后是一个以反演中心位似的圆。

从上面的图来看，显然两个圆是反过来对应的，并不是直接位似。还有切记，圆心反演完以后并不是反演完的圆的圆心，比如上面的点 $H$ 和 $I$。

再来一个好玩点的：

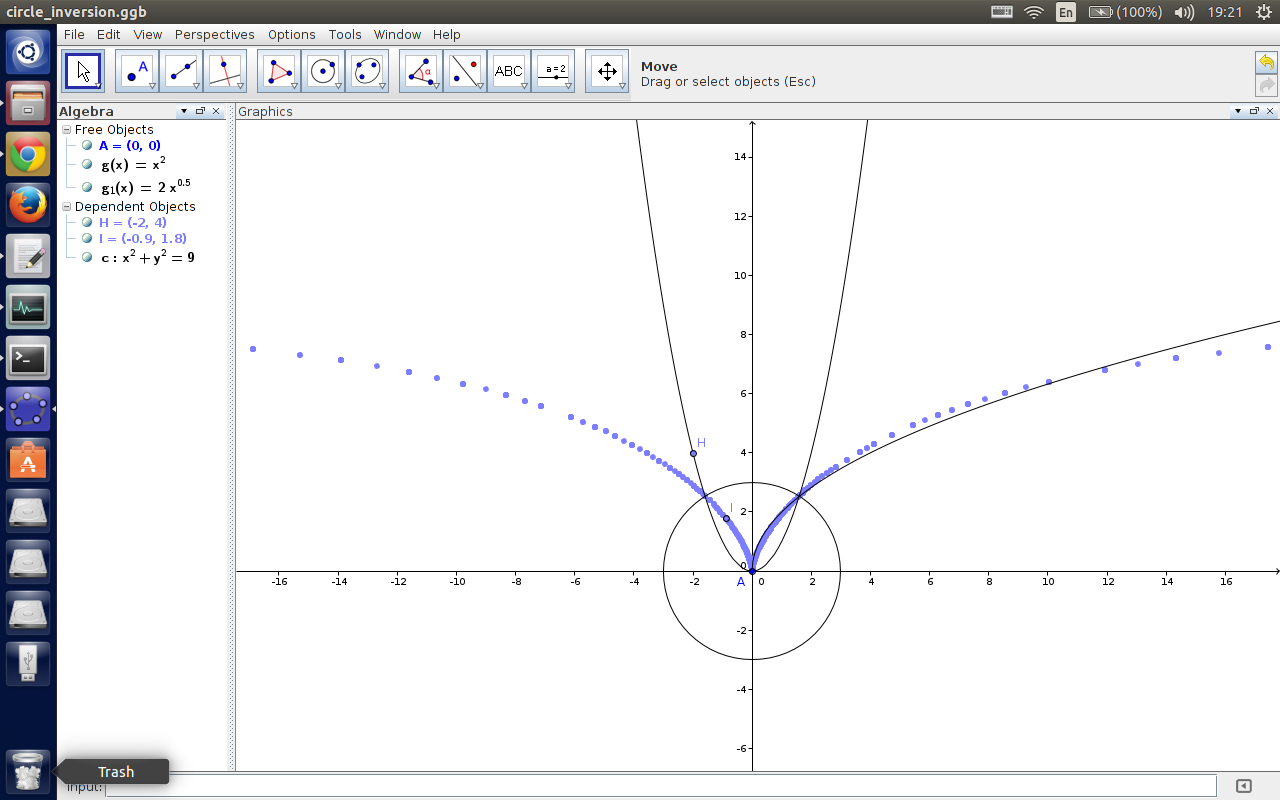
抛物线反演一下，不知道变成了什么。。。右边的黑线是 $2\sqrt{x}$，然而不能拟合。

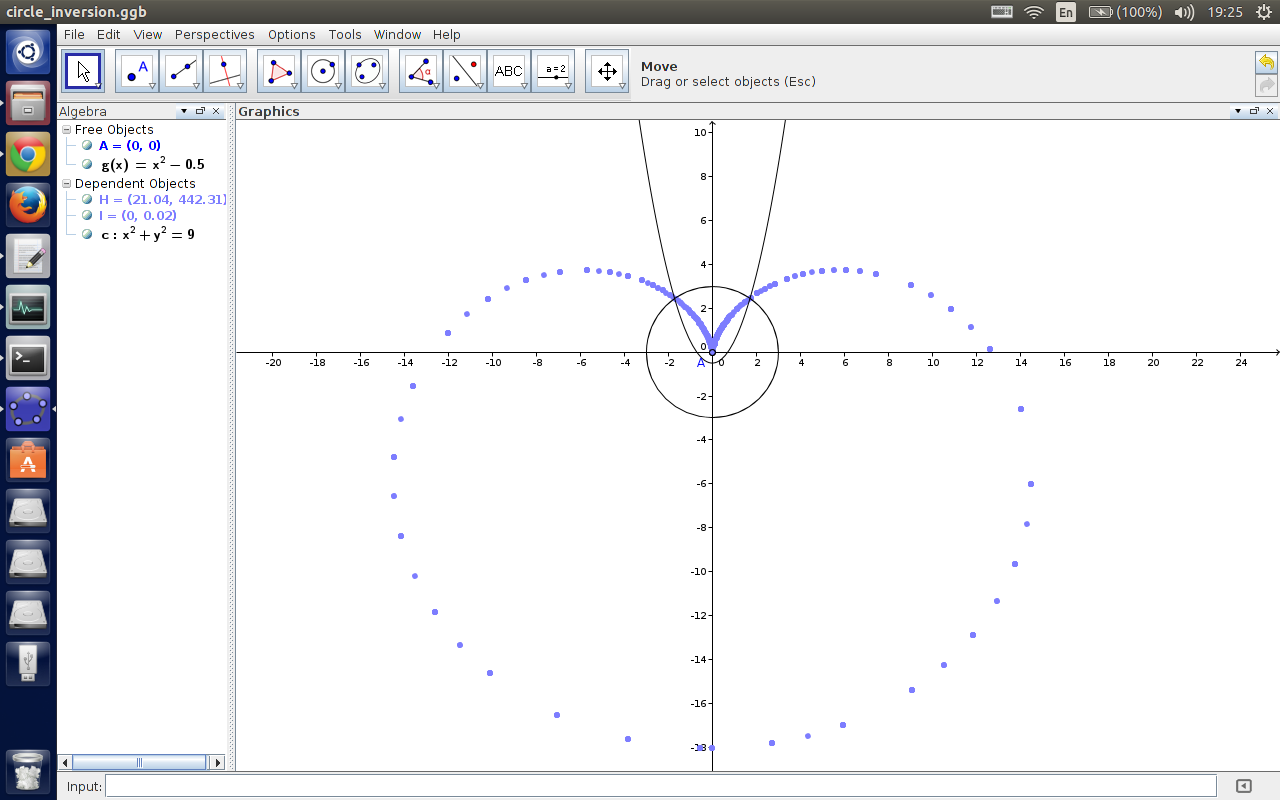
然后稍微往下移一点就变成了心型线！

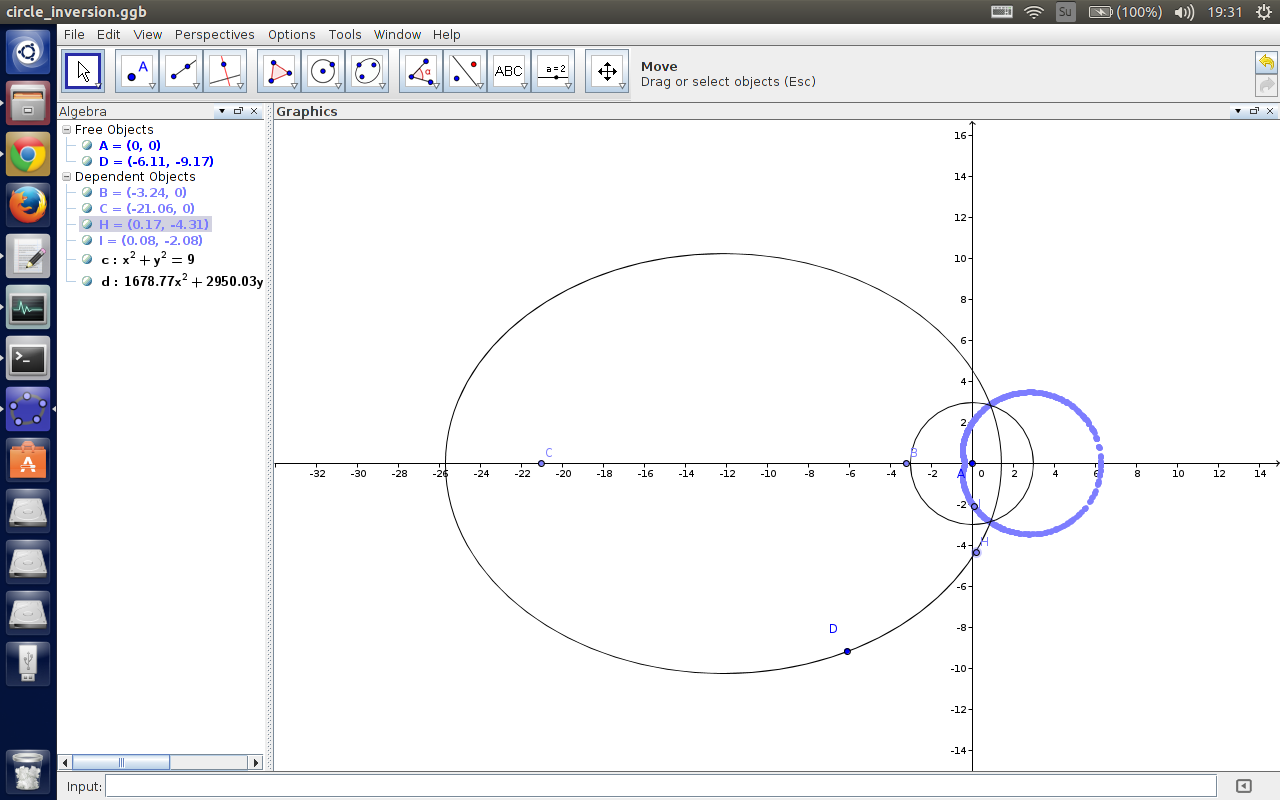
椭圆好像跟上面两种差不多，不是太好玩。

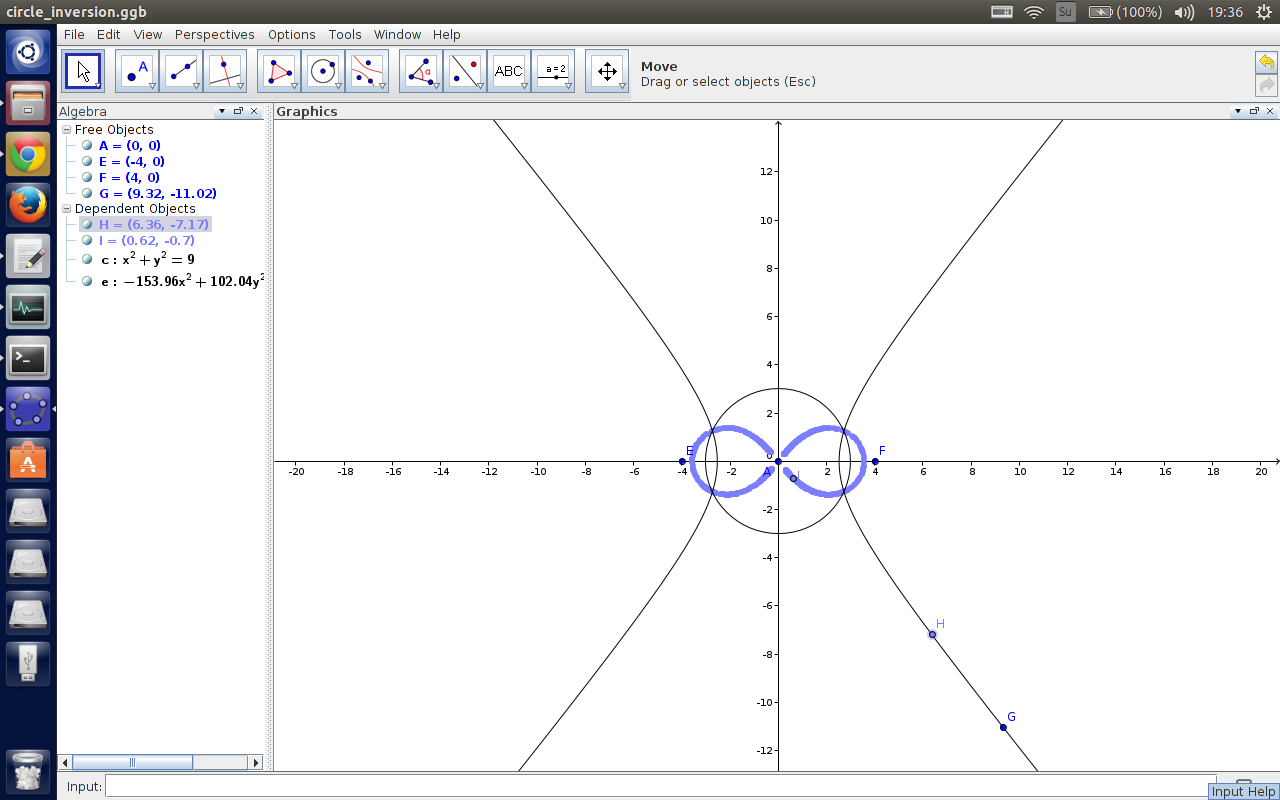
双曲线反演一下变成了 $\infty$...

我们不妨把样例反演一下变成下面这样：

由于反演前后的几何性质是不会发生改变的，比如反演前两个圆相切，反演完以后他们两个还是相切，只不过可能不是圆与圆相切而是直线与圆相切之类的，因此我们可以像这张图这样建立反演中心，圆 $C_1,C_2$ 反演完以后就变成了两条直线，而 $C_3,C_4,\cdots$ 反演完之后，由于没过反演中心，所以还是圆；又因为它们都与圆 $C_1,C_2$ 相切，所以反演以后的圆统统都被夹在了两条直线里面，大小都一样，而且一个挨着一个。

这里详细讲了怎么求一个圆的反演

然而我觉得如果不会求的话，可以随便找圆上的三个点，然后把这三个点反一下，然后再以这三个点画个圆就好了，简单粗暴= =

注意不能直接求圆心。原因在上面第二张截屏。

于是这题的解法已经十分明了了：先把 $C_1,C_2$ 反成直线，解三角形解出 $C_3$ 的位置，然后反成小圆，看一下 $C_4$ 塞哪里符合题意，然后就可以 $O(1)$ 求出第 $n$ 个圆反演完以后的圆，直接反回去就好了。